O sistema de suspensão mostrado abaixo tem o nível da superfície da estrada como entrada e a posição absoluta como saída.

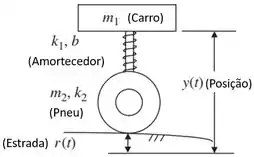
A função de transferência do sistema é:

Dependendo do uso, a massa do carro pode dobrar. Gere em um mesmo gráfico o diagrama de Bode para . Assuma que , , e .

O primeiro passo é entrar com os dados de massa, rigidez e amortecimento do enunciado. Em um script novo, entre com os valores de , , e :

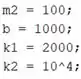
Abaixo dos dados que você acabou de digitar, inicie um laço , com variável de controle , representando a massa do carro. Essa variável de controle deve ir de a , pois o enunciado pede para vermos o diagrama de Bode de para :

O passo da faixa de valores de você pode escolher o que quiser. Eu escolhi , de forma que em assumirá três valores distintos: , e . Isto fará que o meu gráfico com os diagramas de Bode no final tenha três curvas, uma para cada valor de .

Vamos entrar com dentro do laço , escrevendo dentro dele o comando , que tem como sintaxe:

A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .

Vamos criar dois vetores, dentro do laço , contendo os coeficientes dos polinômios do numerador e do denominador de . O polinômio do numerador é e seus coeficientes serão armazenados em um vetor chamado . Já o polinômio do denominador é:

Seus coeficientes serão armazenados em um vetor chamado . Desta forma, o laço tem essa cara por enquanto:

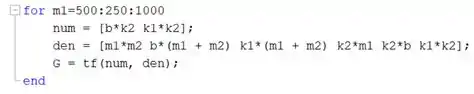
Logo abaixo dos vetores, já podemos incluir o comando , para criar a variável , que contém .

Com o laço de repetição , os vetores e serão atualizados a cada iteração, com um valor de diferente, gerando, portanto, uma função de transferência diferente.

Para gerar o diagrama de Bode para cada função de transferência diferente, utilize dentro do laço o comando , que tem a sintaxe:

Ele tem como entrada uma função de transferência (representada pela variável ), criada usando o comando , e ele gera um gráfico com o diagrama de Bode para .

Logo, acrescente o comando dentro do laço :

Abaixo de , inclua o comando . Este comando serve para que o gráfico com o diagrama de Bode seja atualizado a cada iteração, mas sem que as curvas da iteração anterior desapareçam.

Pra finalizar, coloque logo abaixo do laço o comando:

Ele fará com que o gráfico com os diagramas de Bode tenham uma legenda, indicando qual curva representa o resultado para determinada massa. As legendas dentro de devem estar na ordem com que os diagramas foram criados.