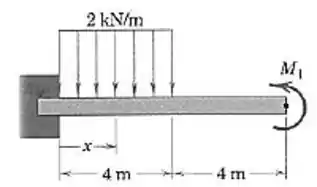
Desenhe os diagramas de cortante e de momento para a viga em balanço carregada, para a qual o momento é ajustado de modo a produzir um momento nulo na extremidade engastada da viga. Determine o momento fletor em
Passo 1
Vamos primeiro calcular a força resultante do carregamento distribuído:
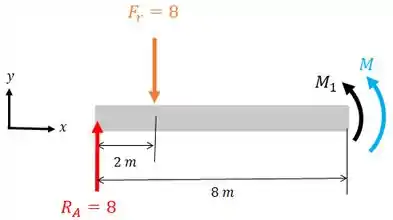
Então, temos o seguinte diagrama de corpo livre:
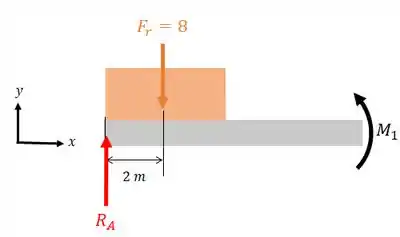
Repare que a força resultante fica localizada na metade do comprimento do carregamento distribuído, ou seja, a do engaste!
Vamos primeiro calcular a reação na parte engastada:
E quanto vale o momento Vamos fazer o somatório de momentos com relação ao engaste considerando o momento girando no sentido anti-horário como positivo:
Repare que não colocamos momento como reação no engaste, pois o enunciado disse que o momento deve ser nulo!!!
Passo 2
Agora vamos achar o cortante . Para isso vamos fazer uma seção em :
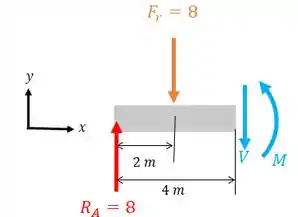
Para achar o cortante nesta seção, vamos fazer o somatório de forças verticais:
Ou seja, na parte que cortamos a viga o cortante é zero. Mas tem o cortante na parte inicial da viga devido à reação de apoio . Vamos analisar seu sinal:
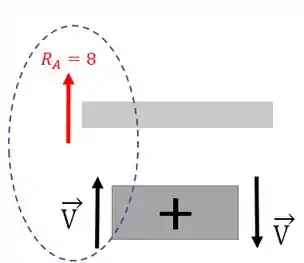
Repare que o cortante é positivo, pois aponta no mesmo sentido do cortante positivo.
E o momento fletor ? Vamos usar o somatório de momentos com relação ao ponto :
Vamos analisar seu sinal:
Repare que o momento fletor é positivo!
Passo 3
Agora vamos analisar o que acontece no final da viga:
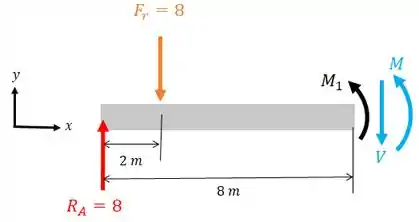
Para calcular o cortante é só fazermos o equilíbrio de forças:
Ou seja, o cortante continua sendo zero até o final da viga.
Como há um momento concentrado no final da viga, sabemos que vai ter uma descontinuidade do momento fletor. Então vamos analisar qual é o momento fletor um infinitésimo antes do momento :
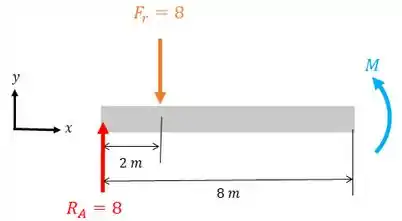
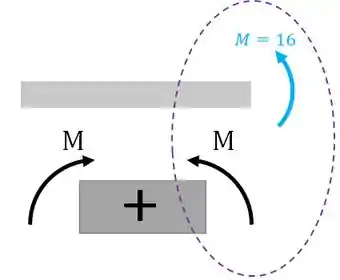
Vamos fazer o somatório de momentos com relação ao ponto :
E o seu sinal será positivo, pois:
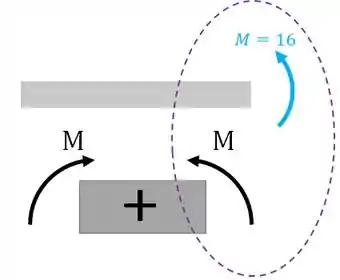
Agora vamos fazer uma seção um infinitésimo depois de do momento de modo a incluí-lo:
Esse momento fletor pode ser calculado pelo somatório de momentos com relação ao ponto de novo:
Ou seja, o momento fletor agora é zero!!!
Passo 4
Agora só falta uma coisinha... Lembra que o cortante é obtido integrando a equação do carregamento que estiver na viga e o momento fletor é obtido integrando a equação do cortante?
Como o carregamento é uma reta constante, o cortante vai ser uma reta que varia linearmente e o momento fletor vai ser uma parábola do segundo grau!
Sabemos que o cortante fica assim:
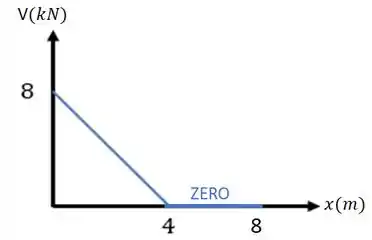
Vamos achar a equação desta reta. Sabemos que ela terá a seguinte forma:
Podemos calcular através da tangente do ângulo de inclinação da reta:
Mas repare que a reta está decrescendo, ou seja, o nosso será negativo:
Quando temos que , então:
Ou seja, a equação do cortante é:
Agora para achar a equação do momento fletor temos que integrar esta equação ao longo do comprimento da viga:
Agora sim podemos desenhar o diagrama do momento fletor:
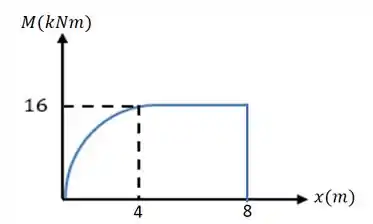
Passo 5
Quando é só substituirmos o valor de nas equações de cortante e momento fletor que acabamos de achar:
E o momento fletor fica: