Construa os diagramas de cortante e de momento para a viga carregada pelas cargas pontual e distribuída. Quais são os valores do cortante e do momento em ? Determine o momento fletor máximo .
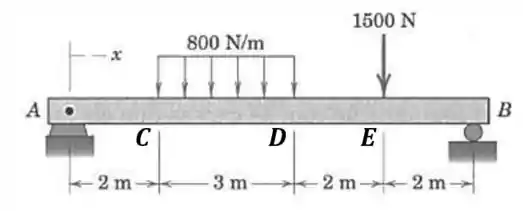
Passo 1
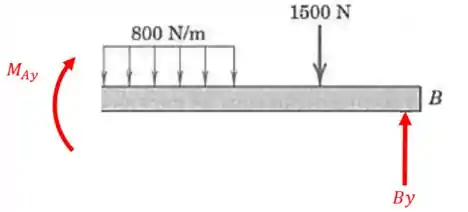
Vamos começar fazendo o diagrama de corpo livre e como temos uma carga distribuída, vamos achar a resultante dela:
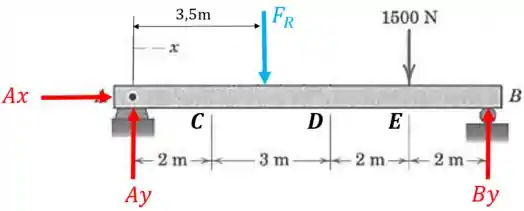
Agora podemos começar o equilíbrio calculando o momento com relação ao ponto :
E por fim o somatório de forças em cada eixo:
Passo 2
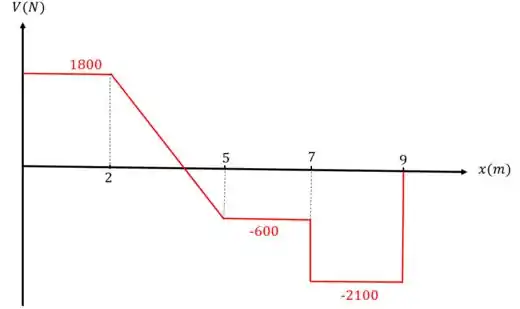
Onde tem reação de apoio tem descontinuidade do cortante, então nos pontos e o cortante vai de zero ao valor da reação:
Sendo que no ponto B, a reação aponta no sentido contrário do cortante positivo, então:
E o momento fletor nesses pontos? Como temos apoios que não impedem a rotação e estão na extremidade da viga sem nenhum momento concentrado sobre eles, então o momento nesses pontos é nulo:
Passo 3
Lembra que se temos a equação do cortante é só derivarmos para achar a equação do carregamento?
Só que não temos a expressão do cortante, pois é justamente o que queremos saber. Mas... temos o carregamento!!!
Nossa carga distribuída é retangular, logo a sua equação é uma constante e vale:
Para achar a equação do cortante a partir dessa equação é só integrarmos e multiplicar por , assim:
Lembra desse ? É a nossa constante de integração e temos que colocar toda vez que não temos um intervalo de integração definido.
Para acharmos seu valor, temos que saber quanto vale o cortante , ou seja, bem onde começa a carga distribuída, porque é fácil sabermos o cortante neste ponto.
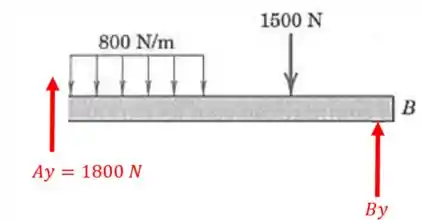
Repare que do ponto até o ponto não há mais nenhuma força, então o cortante neste trecho é constante e vale o mesmo valor do cortante em pela direita.
Então, quando . Vamos substituir isto na fórmula de que achamos:
Então, a expressão do cortante para o trecho de carga distribuída é:
Passo 4
Então, quanto vale o cortante no ponto ? É só substituirmos o valor de :
Perceba que no trecho entre os pontos e não tem nada, então o cortante é constante neste trecho e com o valor de . Então, ao fazer uma seção no ponto :
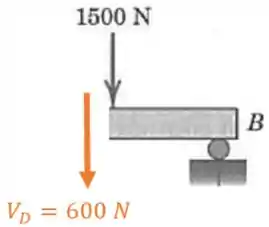
Qual é a resultante do cortante neste ponto, então?
Passo 5
Lembra que derivando a equação do momento fletor obtemos a equação do cortante? Então, vamos fazer o processo inverso já que temos a expressão do cortante para o trecho .
Para achar o valor da constante temos que saber quanto vale o momento fletor em
, que é um ponto fácil de calcular:
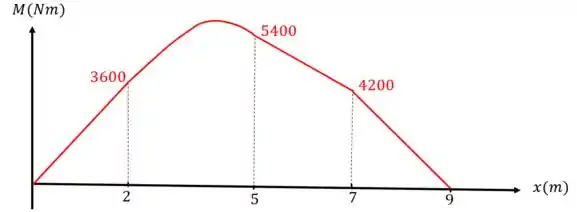
Então, o momento fletor no ponto é:
Quando , vamos substituir isso na equação
Então, a equação do momento fletor no trecho é:
Passo 6
Para saber o momento fletor no ponto é só substituir na equação do momento:
Passo 7
Para calcular o momento fletor no ponto , é só vermos o momento que a reação e a força resultante faz com relação a este ponto:
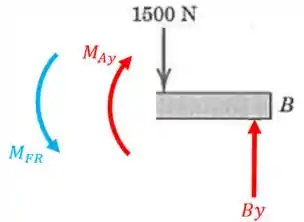
Então, o momento fletor no ponto é :
Passo 8
O nosso diagrama do cortante, vai ficar:
O diagrama de momento fletor, vai ficar assim:
Passo 9
Feito os diagramas, podemos responder quais são os valores do cortante e do momento em
.
O cortante será:
Para sabermos o momento, vamos achar a equação da reta naquele trecho . Sabemos que é uma equação do primeiro grau da forma: e que quando:
Então nossa equação será:
Então, quando :
Passo 10
Para finalizar, vamos achar o momento máximo. Perceba que ele ocorre no trecho , então vamos derivar a equação do momento deste trecho e igualar à zero:
Sabemos que o momento máximo ocorre em , agora temos que achar o valor deste momento: