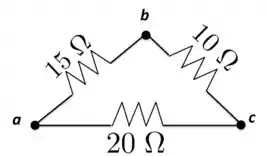
Uma combinação triangular de resistores é indicada na Figura abaixo. Qual é a corrente que essa combinação consumirá de uma bateria de , com resistência interna desprezível, quando ela é conectada através dos pontos :
- ;
Passo 1
a) Quando a bateria é conectada entre os pontos e , temos o resistores de e de em série e o resultado dessa associação em paralelo com o resistor de .
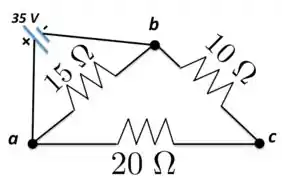
Então, a primeira coisa que precisamos calcular aqui é a resistência equivalente desse circuito. Nesse caso, o resistor resultado da associação entre os resistores e o de é
Esse resistor está em paralelo com o de . Por isso, teremos o seguinte:
Portanto, a corrente do circuito nesse caso é
Passo 2
b) Agora, neste caso, o resistor de é que estará em paralelo com o resultado da associação em série dos resistores de e de . O valor dessa associação em série é .
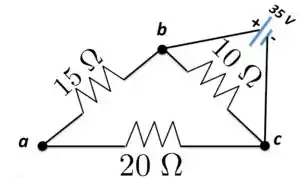
Portanto, a associação em paralelo terá resistência equivalente a
A corrente é, então,
Passo 3
c) Aqui, de maneira semelhante a dos casos anteriores, os resistores de e o de estão em série e tem resistência equivalente dada por .
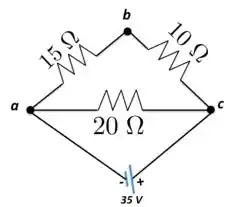
A resistência equivalente do circuito todo será
Então, a corrente será