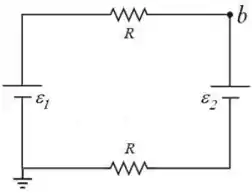
Considere o circuito da figura onde é feito um aterramento no ponto . O valor das resistências é e o das tensões são e . O valor do potencial no ponto em relação ao potencial zero do ponto de aterramento é:

Como temos um circuito de uma única malha, vamos começar aplicando a lei das malhas partindo do ponto onde está o aterramento (de potencial ) e percorrer a malha até o ponto , de potencial da figura. Fazendo isso, teremos:

Para encontrar , precisamos encontrar a corrente . Para isso, vamos percorrer agora toda a malha do circuito saindo do ponto onde (onde está o aterramento) e voltando para esse ponto. Pela lei das malhas, teremos:

Isolando e colocando os valores dados no enunciado:

Substituindo em , temos:

que é a diferença de potencial do ponto em relação ao ponto onde está o aterramento para o qual se tem .