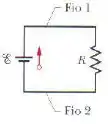
A figura abaixo mostra um resistor de resistência ligado a uma fonte ideal de força eletromotriz através de dois fios de cobre. Cada fio tem de comprimento e de raio. Até então sempre desprezamos a resistência dos fios de ligação. Verifique se a aproximação é válida para o circuito da imagem, determinando:
- a diferença de potencial entre as extremidades do resistor;
- a diferença de potencial entre as extremidades de um dos fios.
- a potência dissipada em um dos fios;
Dados:
Passo 1
a)
Bem, temos que demonstrar nessa questão o porquê de podermos desprezar a resistência nos fios. Então vamos à caça dessa demonstração respondendo as alternativas.
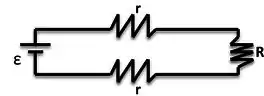
Considerando a resistência de cada fio de cobre, e concentrando-as em dois lugares,a gente vai ter algo mais ou menos assim:
Passo 2
Aplicando a Lei das Malhas de Kirchhoff com uma corrente no sentido horário, teremos:
Passo 3
Mas como que calcula o ? Você se lembra? Eu sim, haha!
Pela Lei de Ohm a gente tinha lá a seguinte relação:
Como o fio é circular, o
Logo, a corrente vai ser:
Passo 4
Agora sim, achando a diferença de potencial nas extremidades do resistor, basta fazer
Viu como fica próximo de 12V? Só assim já provamos que é quase desprezível ter ou não ter considerado a resistência de cada fio.
Mas vamos lá seguindo na questão!
Passo 5
b)
Basta fazer a mesma coisa que fizemos no passo anterior só que pra resistência menor.
Bora lá!
Ou seja, eles tiram uma voltagem super mini do circuito. Desconsiderar seria bem ok. :}
Passo 6
A potência dissipada em um fio de cobre, será dada por:
Também super mini potência.
Moral da história? Pra fios pequenos, como esse, de apenas vale a pena desprezar a resistência.
Mas isso sempre é válido? Não! Por exemplo o fio que liga a hidrelétrica até a sua casa são milhares de kilômetros de distância e a energia dissipada seria beeeem maior!