Determine o valor do potencial nos pontos de a até d da figura
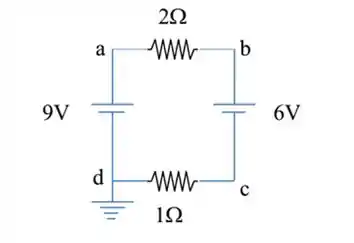
Passo 1
Olhar para as duas baterias e, olhando para elas, determinar cada DDP:
Passo 2
Como a gente tem uma única malha fechada no circuito, a corrente que passa no resistor de é igual à corrente que passa no resistor de :
Passo 3
Aplicar em cima do passo a lei de Ohm:
Passo 4
No passo a gente conseguiu uma nova equação! Vamos juntar ela às equações do passo e resolver o sistema:
Logo:
Assim: