A solução de é
(a)
(b)
(c)
(d)
(e) nenhuma das outras alternativas
Passo 1
Essa equação é separável! Então fazendo , vamos escrevê-la na forma que já estamos mais acostumados de trabalha, tranquilo?
Colocando pra o lado esquerdo tudo o que está em função de e do lado direito tudo o que está em função de
Passo 2
Integrando dos 2 lados:
Para a integral do lado esquerdo temos
Pra outra integral vamos ter
Que vem a partir de
No nosso caso, , tranquilo? Enfim, justando os dois resultado temos
Juntando as duas constantes, podemos chamar de
Passo 3
Agora precisamos isolar o pra isso, podemos aplicar o exponencial dos dois lados, assim tirando o de dentro do
Aplicando a exponencial:
Podemos abrir a exponencial do lado direito lembrando que
Vamos lembrar de não é nada mais que outra constante, com isso chamaremos agora de por que sei lá! Quero dar uma variada e chamar de . Como é uma constante, podemos chamar de qualquer letra, então fica a escolha do freguês! Rsrs.
Além disso, podemos tirar o módulo, já que essa constante pode ser, tanto positiva quanto negativa.
Show! Achamos a solução geral da EDO, agora temos que ver quando , pra descobrirmos o valor da nossa constante que chamamos de .
Passo 4
Vamos ter
Substituímos o por zero e igualado tudo a zero.
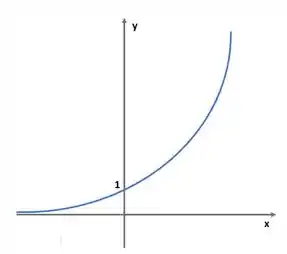
Podemos observar pelo gráfico de exponencial que a curva da exponencial SEMPRE é positiva, certo? Logo, pra essa igualdade estar dando zero (), precisamos que
Logo
Assim, nossa solução se torna:
Resposta
Alternativa (a)