Se é a solução do problema de valor inicial
Então é errado afirmar que
- é limitada
- é decrescente
- para todo
Passo 1
Pelo que conhecemos de EDO, seria excelente se esta fosse separável, não é mesmo?!
Vamos tentar escrevê-la neste formato charmoso:
Passando o para o outro lado temos
Opa, isso é justamente que queremos!
Pronto! Ela é separável !!
Passo 2
Passando para o lado esquerdo tudo o que está em função de e para o lado direito tudo o que está em função de
Passo 3
Agora, integramos os dois lados.
A integral do lado esquerdo pode parecer complicada, mas na verdade é só um polinômio.
Observa que
Com isso podemos reescrever aquilo como
Agora vou precisar que você lembre da integral do polinômio, onde
No nosso caso, . Então teremos
Como o expoente está negativo, vamos colocar o no denominador pra ele ficar positivo.
Pronto, essa foi!
Para resolver a outra integral só precisamos lembrar da integral do exponencial, que é igual a ele mesmo!
Passo 4
Juntando os resultados que obtivemos.
Somando as constantes, vamos chamar simplesmente de , e ficamos então com
Passo 5
Agora vamos isolar o certo?
Começamos multiplicando cruzado
Passamos agora o termo que está multiplicando o , dividindo para o outro lado
Passo 6
Agora só falta resolver o P.V.I. para podermos descobrir o valor da constante . Aplicando que ()
Isolando então o
Já que descobrimos que a constante vale zero, podemos escrever como
Colocando esse exponencial no numerador só pra ficar bonitinho, lembrando da propriedade
Temos
Passo 7
Para podermos fazer a análise que o enunciado nos pede vamos precisar lembrar de como é o gráfico da exponencial
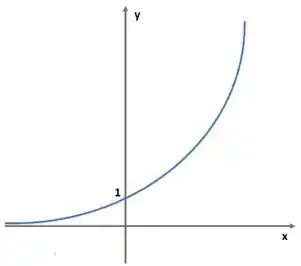
Mas nós estamos trabalhando com , certo? Esse menos na frente do faz com que nos tenhamos que simplesmente espelhar a função em relação ao eixo . Ficamos então com
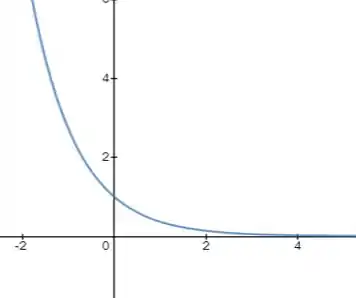
Observando então as opções, vemos que a letra (b) nos diz que a função é limitada! O que não é verdade! Ela vai desde menos infinito até mais infinito tranquilamente! Então essa é a opção errada
Resposta
A letra (b) é errada.