Para um canal retangular de largura b = 20 m, construa uma família de curvas de energia específica para Q = 0,25, 75, 125 e 200 m³/s. Quais são as energias específicas mínimas para essas curvas?
Passo 1
Nesse exercício, vamos entender melhor o comportamento da energia específica no canal retangular.
Escrevendo a equação da energia em função da profundidade do escoamento e considerando que a pressão não variae que não há perda por atrito, temos
Podemos escrever a energia em função da vazão, usando . Como nosso caso é um canal retangular
E assim, atualizando a equação da energia
Sabemos que g é a gravidade e o comprimento b é 20 m
Bem, essa é a equação, mas o enunciado pede uma família dela! Vamos conseguir várias curvas pois para cada uma delas vamos substituir uma vazão Q diferente (também dada no enunciado). Beleza?
As curvas da família são
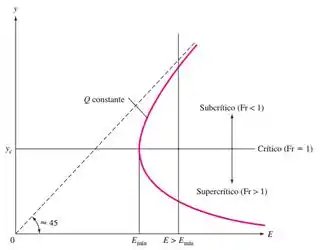
Lembrando que o formato geral dessas curvas é
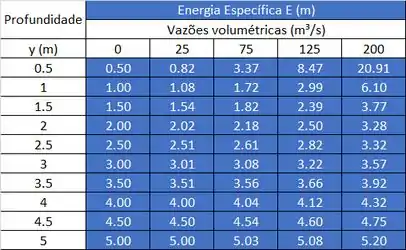
Para fazer as diferentes famílias de curvas, vamos montar uma tabela com as energias específicas para cada vazão volumétrica.
Com isso, já podemos montar o gráfico. Mas antes, atenção! A energia específica fica no eixo x e a profundidade no eixo y! Se colocar ao contrário, o formato da curva vai ficar diferente. Vamos ficar atentas!
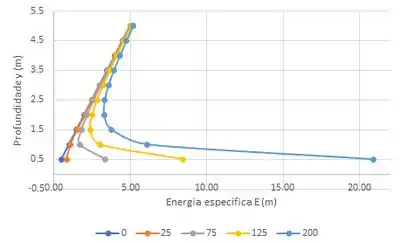
A forma dessas curvas é a mesma que vimos na teoria. Deu tudo certo! Repara que quanto maior a vazão, maior é a energia específica mínima (o ponto em que a curva muda de direção)
Passo 2
O exercício também pediu a energia específica mínima de cada curva. Como se trata de uma energia mínima, ela está associada ao ponto em que a derivada é zero, certo? Logo, é energia específica da profundidade crítica
A profundidade crítica do canal retangular é
Substituindo na equação da energia para o canal retangular de 20 m de comprimento
Organizando
Para
Para
Para
Para
Para
E assim, vemos que quanto maior a vazão, maior a energia específica mínima associada ao ponto crítico, conforme esperávamos pelo gráfico.
Resposta
Ei, a resposta está no passo a passo :)