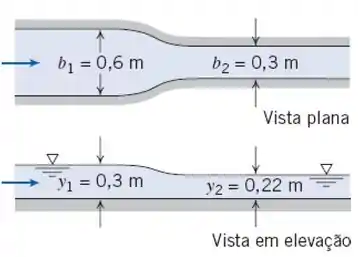
Considere o canal condutor Venturi mostrado. O fundo é horizontal e o escoamento pode ser considerado sem atrito. A profundidade a montante é 0,3 m e a profundidade a jusante é 0,22 m. A largura a montante é 0,6 m e a largura da garganta é 0,3 m. Estime a vazão através do conduto.
Passo 1
E aí! Como o escoamento é sem atrito, vamos usar a equação de Bernoulli (que é a equação da energia sem perdas)
Lembrando que aqui em escoamento aberto trabalhamos com a profundidade y e vamos considerar que nas regiões 1 e 2 temos a mesma pressão (atmosférica)
As velocidades podem ser escritas em função da vazão volumétrica, que é quem queremos calcular
Então substituindo na equação da energia
Agora podemos substituir os dados e encontrar a vazão Q
Resolvendo
Encontramos a vazão volumétrica