Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Específica e escoamento sobre elevação

Ver Teoria
Exercício 71234568

Enunciado

Uma comporta parcialmente aberta em um canal retangular de 5 m de largura carrega água a 10 m³/s. A profundidade a montante é de 2,5 m. Determine a profundidade a jusante e o número de Froude.

Passo 1

Para entender melhor a situação do exercício, vamos ver a figura

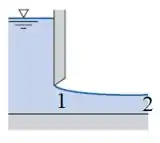
Como a comporta está parcialmente aberta isso permite que o escoamento aconteça logo a seguir, e esse é um escoamento em canal aberto, que estamos estudando agora

A profundidade a montante é a profundidade da região 1, onde começa o escoamento. Ou seja, pelo enunciado

y 1 = 2,5   m

O exercício quer saber a profundidade a jusante, ou seja, y 2 e o número de Froude.

Vamos encontrar a profundidade primeiro, utilizando a equação da energia

y 1 + V 1 ² 2 g + p 1 ρ g = y 2 + V 2 ² 2 g + p 2 ρ g + h p

Como não há informações sobre perdas, vamos considerar escoamento sem atrito. Além disso, vamos considerar nas duas regiões a pressão é a mesma (aberto a atmomsfera)

Com isso a equação da energia fica mais simples

y 1 + V 1 ² 2 g = y 2 + V 2 ² 2 g

Lembrando que a velocidade pode ser escrita em função da vazão volumétrica, que foi dada

V = Q A = Q b y

y 1 + Q b y 1 2 2 g = y 2 + Q b y 2 2 2 g

y 1 + Q 2 2 g b y 1 2 = y 2 + Q 2 2 g b y 2 2

Substituindo y 1 , Q e b (do enunciado)

2,5 + 10 2 2 × 9,8 5 × 2,5 2 = y 2 + 10 2 2 × 9,8 5 × y 2 2

Resolvendo

2 , 5327 = y 2 + 0,204 y 2 2

( 2,5327 ) y 2 2 = y 2 3 + 0,204

y 2 3 - 2,5327 y 2 2 + 0,204 = 0

y 2 = 0,302   m

Encontramos a profundidade a jusante!

Passo 2

O número de Froude é

F r = V V o n d a = V g y

Como queremos saber o número de Froude a jusante F r 2

F r 2 = V 2 g y 2

Acabamos de encontrar a profundidade a jusante. Para achar a velocidade, vamos usar V = Q/A novamente

V 2 = Q b y 2

Então Froude é

F r 2 = Q b y 2 1 g y 2

Substituindo

F r 2 = 10 5 × 0,302 1 9,8 × 0,302

F r 2 = 3,85

Resposta

y 2 = 0,302   m

F r 2 = 3,85

Exercícios de Livros Relacionados

Um vertedor de soleira delgada retangular com contração final tem 1,5m de comprimento. A que altura deveria a crista do vertedouro ser colocada em um canal para manter uma profundidade a montante de 2
Em uma seção de um canal retangular com 3m de largura, a profundidade é 0,09m para uma descarga de 0,57m 3 / s . Um ressalto suave com 0,03m de altura é colocado sobre o fundo do canal. Determine a va
Considere o canal condutor Venturi mostrado. O fundo é horizontal e o escoamento pode ser considerado sem atrito. A profundidade a montante é 0,3m e a profundidade a jusante é 0,22m . A largura a mont
A figura mostra o escoamento através de uma comporta. Estime a profundidade da água e a velocidade depois da comporta (bem antes do ressalto hidráulico).
Água é descarregada de uma comporta a uma profundidade de 1,25m . A descarga por unidade de largura é 10m 3 / s / m . Estime o nível de água longe a montante onde a velocidade do escoamento é desprezí