Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Específica e escoamento sobre elevação

Ver Teoria
Exercício 81234567

Enunciado

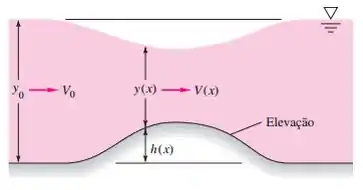
Na Figura, seja V 0 = 1   m / s e y 0 = 1   m . Se a altura máxima da elevação for de 15 cm, calcule (a) o número de Froude sobre o topo da elevação e (b) a depressão máxima na superfície da água.

Passo 1

Vamos falar um pouco agora sobre o escoamento sobre elevações.

Podemos analisar esse problema simplesmente aplicando nossa equação da energia que aplica esta variação de altura:

y 2 ³ - V 0 2 2 g + y 0 - ∆ h y 2 2 + V 0 2 y 0 ² 2 g = 0

Conhecemos

V 0 = 1 m s

y 0 = 1   m

∆ h = 0,15   m

Logo a equação se torna:

y 2 ³ - 1 2 × 9,81 + 1 - 0,15 y 2 2 + 1 2 × 9,81 = 0

y 2 ³ - 0,9 y 2 2 + 0,051 = 0

Podemos resolver esta equação de terceiro grau usando algum método númerico ou podemos realizar uma aproximação que 0,051 ≈ 0 .

Logo,

y 2 3 = 0,9 y 2 2

y 2 ≈ 0,9

Se diminuirmos um pouco este valor de y 2 podemos chegar a um valor mais preciso. Por exemplo se aplicamos y 2 = 0,8 a parte direita da equação se torna - 0,013 , um número mais próximo de zero que o anterior.

Passo 2

Para calcularmos o Froude devemos calcular V 2 , supondo vazão constante:

V 2 y 2 = V 0 y 0

Logo V 2   é

V 2 = V 0 y 0 y 2 = 1 0,8

V 2 = 1,25   m / s

Portanto nosso Froude é igual a

F r = V 2 g y 2 = 1,25 9,81 × 0,8

F r = 0,45

Passo 3

Na letra ( b ) o problema se torna geométrico apenas, sabemos que pela figura:

y 0 = y 2 + ∆ h + ∆ z

Sendo ∆ z a diminuição no nível da superfície livre:

1 = 0,8 + 0,15 + ∆ z

∆ z = 0,05   m

Resposta

a   F r = 0,45

b ∆ z = 0,05   m

Exercícios de Livros Relacionados

Um vertedor de soleira delgada retangular com contração final tem 1,5m de comprimento. A que altura deveria a crista do vertedouro ser colocada em um canal para manter uma profundidade a montante de 2
Em uma seção de um canal retangular com 3m de largura, a profundidade é 0,09m para uma descarga de 0,57m 3 / s . Um ressalto suave com 0,03m de altura é colocado sobre o fundo do canal. Determine a va
Considere o canal condutor Venturi mostrado. O fundo é horizontal e o escoamento pode ser considerado sem atrito. A profundidade a montante é 0,3m e a profundidade a jusante é 0,22m . A largura a mont
A figura mostra o escoamento através de uma comporta. Estime a profundidade da água e a velocidade depois da comporta (bem antes do ressalto hidráulico).
Água é descarregada de uma comporta a uma profundidade de 1,25m . A descarga por unidade de largura é 10m 3 / s / m . Estime o nível de água longe a montante onde a velocidade do escoamento é desprezí