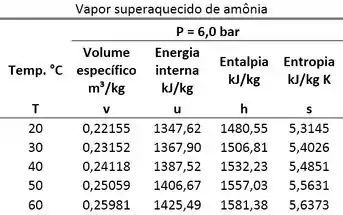
Amônia, inicialmente a e , é submetida a um processo sob volume específico constante até uma pressão final de . Determine, para o estado final, a energia interna específica. Use as tabelas abaixo.
Passo 1
Esse exercício pede que a gente descubra o valor da energia interna específica da amônia, depois dela passar por um processo que mantém o seu volume específico igual. Ou seja, a amônia tinha um estado inicial (estado 1) e, depois de passar por esse processo, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
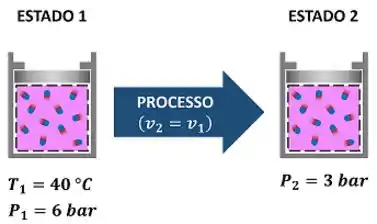
Como podemos achar a energia interna específica do estado 2 se nós só conhecemos o estado 1? Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Mas como faremos isso? Por enquanto só conhecemos a pressão desse estado .

Fazemos isso encontrando o valor de volume específico do estado 1 ! Como o processo mantém o volume específico da amônia igual:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado. A partir daí, achamos a energia interna específica através da tabela de propriedades!
Mas como encontramos o volume específico ?

Temos que descobrir se o estado 1 é saturado ou vapor superaquecido. Se o estado 1 for vapor superaquecido, usamos a tabela de vapor superaquecido. Se o estado 1 for saturado, usamos a tabela de vapor saturado para encontrar ! Para saber isso, comparamos a temperatura de saturação para a água a com sua temperatura .

Caso ela tenha temperatura maior que a temperatura de saturação, ela é um vapor superaquecido!
Caso ela tenha temperatura igual à temperatura de saturação, ela estará saturada.
Passo 2
Já sabemos como descobrir a fase do estado 1 comparando a sua temperatura com a temperatura de saturação . Como podemos descobrir a fase do estado 2, comparando o seu volume específico com os volumes específicos de saturação ( e )?

Se volume específico for maior que volume específico do vapor saturado a , então a amônia é um vapor superaquecido e precisaremos usar a tabela de vapor superaquecido.
Se o valor de estiver entre e , a amônia está saturada.
Se o estado 2 for vapor superaquecido, achamos a energia interna específica olhando a tabela de vapor superaquecido. E se o estado 2 for um estado saturado, como encontramos sua energia interna específica ? Usamos o ou o da tabela de saturação? Caso o estado 2 seja saturado, a energia interna específica tem a seguinte fórmula:
onde é o título do estado saturado 2.
Mas como podemos encontrar o valor de ? Se liga na dica: se queremos encontrar o título da mistura saturada e já sabemos o seu volume específico, podemos usar a fórmula a seguir:
onde é o volume específico do vapor saturado na pressão do estado 2 e é o volume específico do líquido saturado na pressão do estado 2 .
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Começamos as nossas contas, encontrando a temperatura de saturação do estado 1 para ver se esse estado é vapor superaquecido ou saturado. Pela tabela de saturação vemos que:
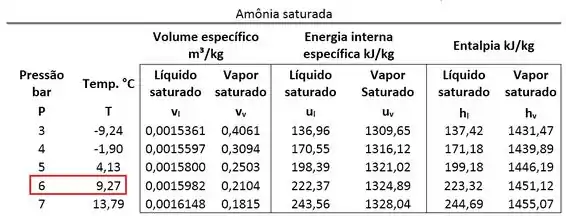
Como a temperatura do estado um vale , concluímos que:
O estado 1 é vapor superaquecido. Isso quer dizer que encontramos o volume específico desse estado olhando para a tabela de vapor superaquecido.
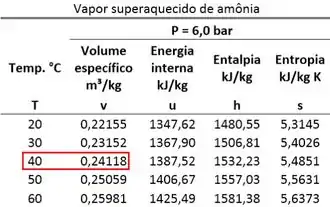
Como o volume específico do estado 2 é igual ao volume específico do estado 1, descobrimos que:
Ou seja, a pressão do estado 2 vale e o volume específico do estado 2 vale . Já fixamos este estado. Agora só falta saber qual é a fase do estado 2 para encontrarmos a sua energia interna específica .
Passo 4
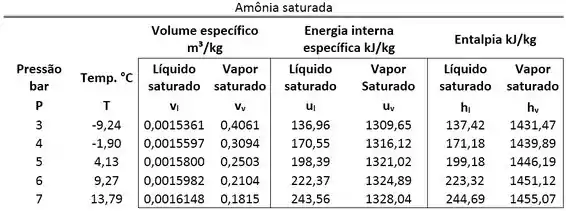
Vemos pela tabela de saturação que os volumes específicos saturados valem:
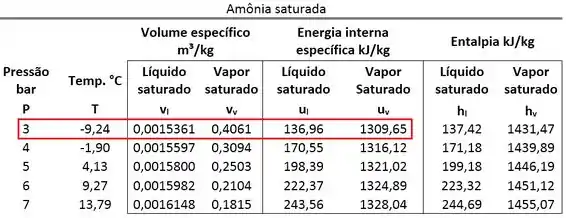
O volume específico do estado 2 está entre esses dois valores. Logo, o estado 2 é saturado. Então, para calcular temos que conhecer o título da mistura saturada.
Nessa tabela, também encontramos também os valores das energias internas de saturação que serão importantes para o cálculo de .
Substituindo esse valor na fórmula de :