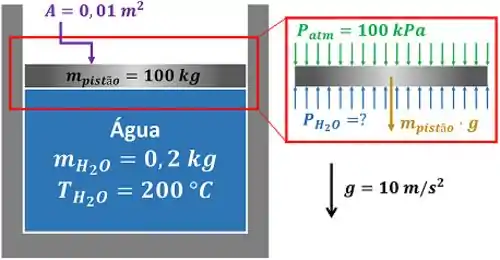
Conforme ilustrado na figura abaixo, um conjunto ciclindro-pistão contém de água a . O pistão está livre para mover-se suavemente no cilindro. A pressão atmosférica e a aceleração da gravidade são de e , respectivamente. Para a água, determine a pressão, em , e a energia interna, em joule . Use as tabelas de propriedades termodinâmicas abaixo.
Passo 1
O primeiro passo para entender essa questão é saber como encontrar a pressão da água. Ela está sendo comprimida por duas coisas: pela atmosfera e pelo peso do pistão. A pressão que a atmosfera faz sobre a água já é dada pelo enunciado.
A pressão que o peso do pistão faz sobre a água é dada indiretamente pelo enunciado. Ela é igual ao peso do pistão dividido pela sua área .
A massa do pistão e a aceleração da gravidade também são informadas.
A pressão total exercida da água deve ser igual à soma dessas duas pressões.
Mas por que a pressão da água deve ser igualzinha á soma dessas duas pressões? Porque o enunciado informa que o pistão está livre para mover-se suavemente no cilindro. Isso significa que a água tem que sustentar o peso da atmosfera mais o peso do pistão para manter o pistão apoiado e equilibrado sobre ela!

Agora que sabemos como calcular a primeira incógnita que o enunciado pede, vamos aprender a calcular a próxima: e energia interna da água .
Passo 2
A primeira etapa para encontrar a energia interna da água é lembrar que ela é igual à energia interna específica vezes a massa da água.
A massa da água é dada diretamente pelo enunciado.
Já a energia interna específica é uma informação que precisamos descobrir através das tabelas de propriedades. O primeiro passo para achar esse valor é descobrindo se a água é um vapor superaquecido ou está saturada. Para saber isso, comparamos a pressão de saturação para a água a com sua pressão calculada no passo anterior.

Caso ela tenha pressão menor que a pressão de saturação, ela é um vapor superaquecido!
Caso ela tenha pressão igual à pressão de saturação, ela estará saturada.
Se ela for saturada, pegamos esse valor da tabela de saturação. Se ela for um vapor superaquecido, pegamos esse valor da tabela de vapor superaquecido.
Encontramos a sua energia interna específica na tabela através da sua pressão e da sua temperatura .
Agora que conhecemos todos os passos para chegar na resposta, vamos iniciar os cálculos!
Passo 3
Vamos começar as contas pela pressão que a massa do pistão exerce sobre a água .
Somando esse valor com a pressão atmosférica, achamos a pressão da água.
Agora vamos calcular a energia interna da água no próximo passo.
Passo 4
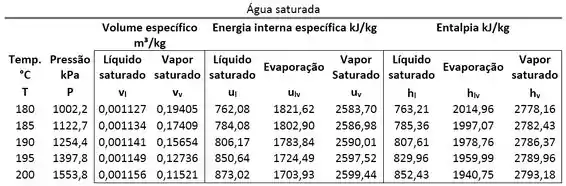
Para descobrir qual é o estado da água, comparamos a sua pressão com a pressão de saturação da água na temperatura de . Para saber qual é a pressão de saturação da água, usamos a tabela de saturação.
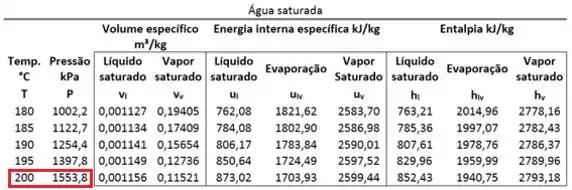
Logo, a pressão de saturação vale:
Ou seja:
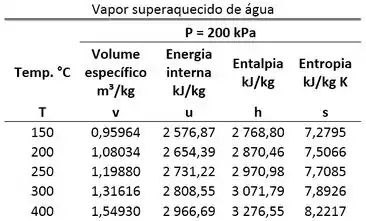
A água é um vapor superaquecido. Então, devemos usar a tabela de vapor superaquecido para achar .
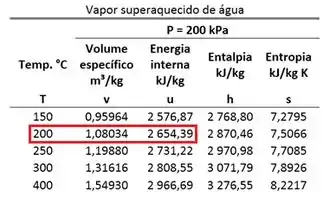
A energia interna específica da água vale:
Atenção, precisamos lembrar de converter a energia interna específica para joule por quilograma ! Como o exercício pede a energia interna da água em joule, essa conversão é necessária para a gente não se confundir depois.
Agora podemos achar a energia interna da água através da sua fórmula.
Pronto, encontramos as duas incógnitas que a questão pede!