Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Interna

Ver Teoria
Exercício 12345678

Enunciado

Determine a energia interna específica da água, usando as tabelas de propriedades dada. Considere o seguinte caso:

T = 190   ° C , V = 1,2   m 3 e m = 10   k g .

Passo 1

Primeiro, para saber qual tabela devemos usar, devemos comparar o volume específico da água v com os volumes específicos do vapor saturado v v e do líquido saturado v l para temperatura igual a 19 0   ° C que estão na tabela de saturação.

O enunciado informa que:

T = 190   ° C

V = 1,2   m 3

m = 10   k g

Porém ele não informa v diretamente. Para calculá-lo, precisamos lembrar que:

v = V m

Temos todos esses valores. Agora é só aprender a descobrir a fase da água para determinar qual tabela vamos usar! Faremos isso na próxima etapa.

Passo 2

Agora vamos aprender a descobrir a fase da água, comparando o volume específico v com os volumes específicos informados pela tabela v l   e   v v !

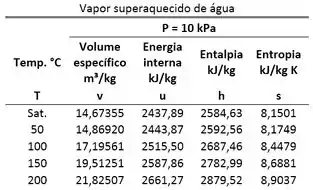
Se volume específico v for maior que volume específico do vapor saturado a 190   ° C v v , então a água é um vapor superaquecido e precisaremos usar a tabela de vapor superaquecido.

S e   v > v v   ⟹   V a p o r   s u p e r a q u e c i d o

Se v for menor que volume específico do líquido saturado a 190   ° C v l , a água é um líquido comprimido. Aí teremos que usar a tabela de líquido comprimido.

S e   v < v l   ⟹   L í q u i d o   c o m p r i m i d o

Por fim, se o valor de v estiver entre v l e v v , a água está saturada.

S e   v l ≤ v ≤ v v   ⟹   S a t u r a ç ã o

Antes de comparar esses valores, precisamos entender a pegadinha dessa questão e alguns outros tópicos. É sobre isso que o próximo passo vai falar!

Passo 3

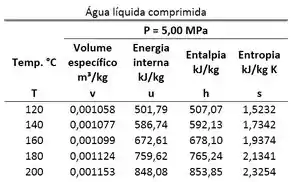
Atenção para a seguinte pegadinha! Ainda não sabemos se podemos usar as tabelas de vapor superaquecido e de líquido comprido, porque elas só podem ser usadas paras as pressões de 10   k P a e 5   M P a respectivamente e ainda não sabemos a pressão da água!

Além dessa pegadinha, devemos nos preocupar em achar o título da água, caso ela esteja saturada! Como podemos fazer isso? Reorganizando a fórmula de volume específico médio para mistura!

x = v - v l v v - v l

Só com esse valor que seremos capazes de calcular a energia interna específica da água caso ela seja uma mistura entre vapor e líquido. Quando ela for uma mistura saturada, a fórmula de energia interna específica vai precisar dessa variável.

u = 1 - x ⋅ u l + x ⋅ u v

Agora vamos encontar os três volumes específicos ( v , v l e v v ) e descobrir qual é a fase da água!

Passo 4

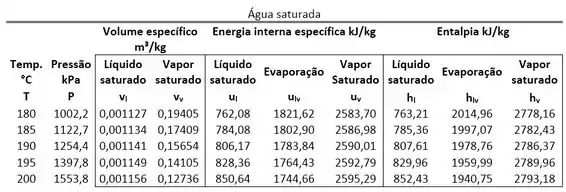
Vemos que para T = 190   ° C os volumes do líquido saturado v l e vapor saturado v v são:

v l = 0,001141   m 3 k g

v v = 0,15654   m 3 k g

Podemos calcular achar o volume específico da água pela fórmula.

v = v m ⟹ v = 1,2 10 ⟹ v = 0,12   m 3 k g

Comparando esse volume específico com volumes específicos de saturação, vemos que:

v l < v < v v

Logo a água está saturada! Ou seja, precisaremos usar apenas a tabela de saturação para descobrir a sua energia interna específica. Como seu volume específico está entre os dois valores de saturação, sabemos também que ela é uma mistura saturada com o título valendo:

0 < x < 1

Ou seja, para calcularmos a sua energia interna específica temos que encontrar o valor do título. E é exatamente isso que faremos na próxima etapa!

Passo 5

x = v - v l v v - v l ⟹ x = 0,12 - 0,001141 0,15654 - 0,001141 ⟹ x = 0,765

Agora só falta obter os valores de energia interna específica saturada através da tabela para encontrarmos o resultado que queremos. Conseguimos cumprir esse passo, olhando para a tabela a seguir:

u l = 806,17   k J k g

u v = 2590,01   k J k g

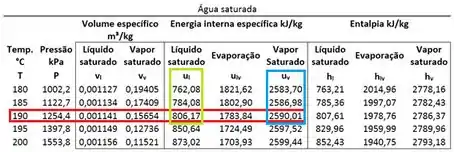
Substituindo esses valores na equação principal, alcançamos o resultado final:

u = 1 - x ⋅ u l + x ⋅ u v

u = 1 - 0,765 ⋅ 806,17 + 0,765 ⋅ 2590,01

u = 2170,81   k J k g

Resposta

u = 2170,81   k J k g

Exercícios de Livros Relacionados

Deduza expressões para ((del u)/(del P))_T e ((del v)/(del T))_P envolvendo somente P , v e T .
A quantidade de calor absorvida quando 1 kg de água líquida saturada ferve a 100 °C é igual à quantidade de calor liberada quando 1 kg de vapor de água saturado condensa a 100 °C?
12 – 52 Mostre que beta = alpha ((del P)/(del T))_v .
61. Um arranjo pistão-cilindro contém inicialmente 1,4 kg de água líquida saturada a 200 °C. Calor é transferido para a água até que o volume quadruplique e o cilindro contenha apenas vapor saturado.
Derive expressões para (a) Δ u , (b) Δ h e (c) Δ s considerando um gás que obedeça a equação de estado P v - a = R T , em um processo isotérmico.