Um tanque rígido fechado contém água inicialmente como vapor saturado a , sendo esta resfriada até . Determine a energia interna final da água. Use as tabelas de propriedades abaixo.
Passo 1
Esse exercício pede que a gente descubra o valor da energia interna específica da água, depois dela passar por um processo. Ou seja, a água tinha um estado inicial (estado 1) e, depois de passar por esse processo, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
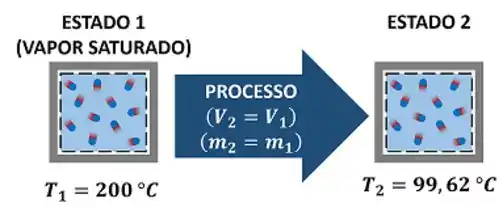
Como podemos achar a energia interna específica do estado 2 se nós só conhecemos o estado 1? Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Mas como faremos isso? Por enquanto, só conhecemos a temperatura desse estado .

Fazemos isso levando em conta algumas informações que estão escondidas no enunciado. A primeira delas é obtida, quando o enunciado fala que a água está contida em um tanque rígido. Se o tanque é rígido, ele permanece com o mesmo volume durante o processo. Ou seja, se o tanque é rígido, o volume que a água ocupa não muda.
A outra informação escondida é obtida na parte em que o enunciado diz que o tanque rígido está fechado. Isso significa que não tem massa de água entrando ou saindo do tanque. Logo, a massa de água não muda.
Como o volume e a massa da água permanecem iguais durante todo o processo, seu volume específico também permanece igual:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado. A partir daí, achamos a energia interna específica através da tabela de propriedades!
Mas como encontramos o volume específico ?

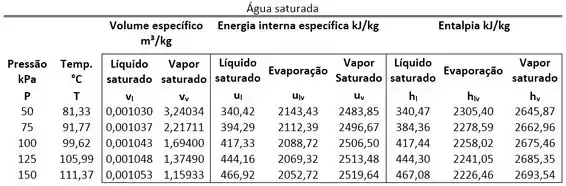
Através da tabela de saturação! Como o estado 1 é vapor d’água saturado, o volume específico é igual ao volume específico que está na linha da temperatura .
Passo 2
Já sabemos a fase do estado 1. Como podemos descobrir a fase do estado 2? Comparando o seu volume específico com os volumes específicos de saturação ( e )!
Se volume específico for maior que volume específico do vapor saturado a , então a amônia é um vapor superaquecido.
Se o valor de estiver entre e , a amônia está saturada.
Se o estado 2 for um estado saturado, como encontramos sua energia interna específica ? Usamos o ou o da tabela de saturação? Caso o estado 2 seja saturado, a energia interna específica tem a seguinte fórmula:
onde é o título do estado saturado 2.
Mas como podemos encontrar o valor de ? Se liga na dica: se queremos encontrar o título da mistura saturada e já sabemos o seu volume específico, podemos usar a fórmula a seguir:
onde é o volume específico do vapor saturado na temperatura do estado 2 e é o volume específico do líquido saturado na temperatura do estado 2 .
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Começamos as contas, encontrando o valor de na tabela de saturação. Antes, precisamos lembrar que o estado 1 é vapor saturado de água.
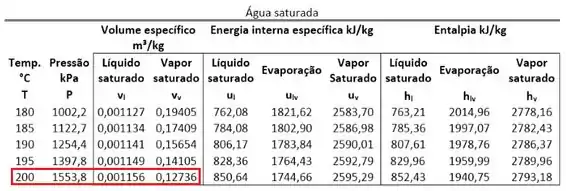
Como o volume específico do estado 2 é igual ao volume específico do estado 1:
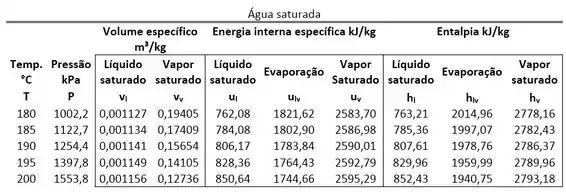
Agora podemos comparar esse valor com os valores dos volumes específicos saturados para saber qual é a fase do estado 2. Para achar e usamos, de novo, a tabela de saturação.
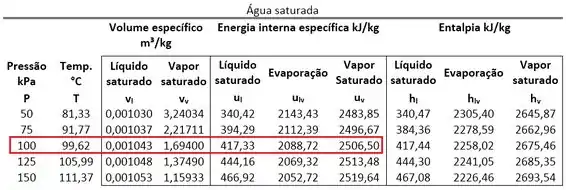
O volume específico do estado 2 está entre esses dois valores. Logo, o estado 2 é saturado. Então, para calcular temos que conhecer o título da mistura saturada. Faremos isso no próximo passo.
Passo 4
Nessa tabela, também encontramos também os valores das energias internas de saturação que serão importantes para o cálculo de .
Substituindo esse valor na fórmula de :