Determine a energia interna de um balde com de água líquida saturada à pressão atmosférica de . Use a tabela abaixo.
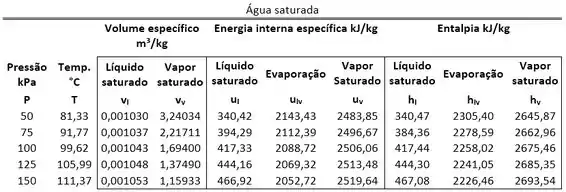
Passo 1
Devemos primeiro visualizar o exercício através da figura do balde de água líquida.
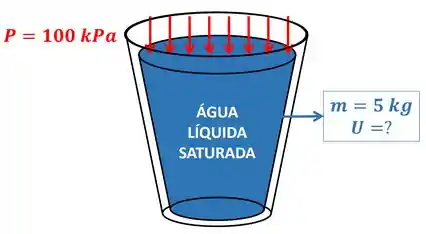
O enunciado pede para a gente encontrar a energia interna de de água líquida saturada, mas a tabela que ele nos deu tem apenas valores de energia interna específica . Como podemos resolver esse impasse? Lembrando da fórmula da energia interna em função da energia interna específica.
Essa fórmula mostra pra gente que para encontrar só precisamos multiplicar pela massa do sistema! Então quanto valem e ? Começando pelo , vemos que o valor de para líquido saturado está na mesma linha que a pressão de e na mesma coluna que .
A massa é informada pelo próprio enunciado:
Vamos encontrar na próxima etapa e depois vamos usar a fórmula para achar .
Passo 2
Como podemos extrair o da tabela? Lembrando que ele fica na mesma linha que a pressão da água e na mesma coluna que .
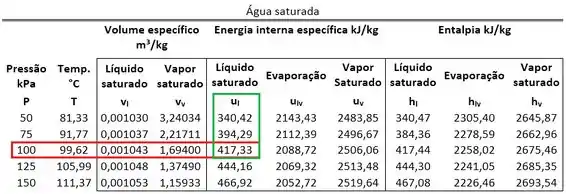
Então:
Sabendo disso, já podemos usar a fórmula de energia interna no próximo passo!
Passo 3
Esse é o resultado que queríamos!