Um bloco de , atrelado a uma mola ideal cuja constante elástica é , oscila sobre uma superfície horizontal sem atrito. Se a energia mecânica total do sistema bloco-mola é , o quadrado do alongamento máximo da mola em relação a posição de equilíbrio é:
A.
B.
C.
D.
E.
Passo 1
Gente, vamos pensar em uma mola oscilando com um bloquinho. O bloquinho vai pra um lado e depois pro outro, certo? Enquanto ele faz esse movimento, onde está o ponto em que a mola fica mais esticada? Se ela tá esticada (alongada) então deve ser o ponto em que o bloquinho tá o mais distante possível, certo? Certo!
Outra coisa que podemos dizer desse ponto distante é que a velocidade do bloquinho é momentaneamente zero, isso porque o bloquinho já tá o mais longe possível, então tá na hora dele começar a voltar, então percebe ele tem que parar pra poder fazer o movimento de voltar pra mais perto da mola?
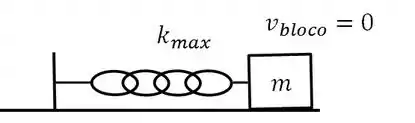
Beleza, então quando a mola tá no seu alongamento máximo, a velocidade do bloco é zero. Em outras palavras, quando a energia potencial elástica é máxima, a energia cinética é zero.
Passo 2
O enunciado pede pra gente calcular o , isso vai ocorrer quando for máximo. Consequentemente, .
Calculando a energia mecânica do sistema Bloco+Mola:
Substiuindo os valores do enunciado:
Ou seja:
Resposta
Alternativa D