Uma mola quando distendida ou comprimida exerce uma força restauradora do tipo , onde é a distensão/compressão da mola, e . Acopla-se um bloco de massa na extremidade da mola.
(a) Calcule uma expressão para a energia potencial elástica dessa mola.
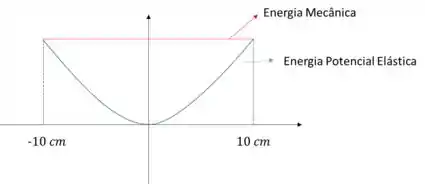
(b) Se distendermos a mola de uma distância de , soltando em seguida, faça o gráfico de , marcando a energia mecânica total do sistema e os pontos de retorno.
(c) Desprezando a existência de forças dissipativas, calcule a velocidade com que o bloco passa pelo ponto de equilíbrio.
(d) Supondo agora que haja atrito e que em uma oscilação completa esta força de dissipação realiza um trabalho de . Calcule a distensão da mola nesta situação.
Passo 1
a) A energia potencial é igual ao trabalho realizado pela mola quando distendida/comprimida. Usando como o tamanho dessa distensão/compressão:
Logo:
Passo 2
b) Seja e energia potencial elástica da mola, temos:
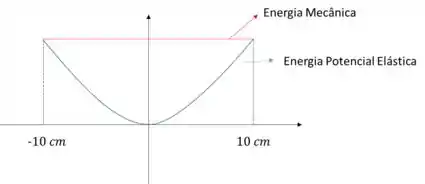
Passo 3
c) No ponto de equilíbrio toda a energia mecânica será cinética
Quando a mola está totalmente distendida a sua velocidade é nula, logo a sua energia é puramente potencial e dada por
Onde é a amplitude do movimento e no nosso caso , segundo o enunciado da letra b.
Como a energia mecânica se conserva, temos que essas duas energias que escrevemos agora são iguais
Substituindo os valores:
Passo 4
d) A situação de oscilação completa começa quando largamos a massa com a mola distendida e termina quando a massa perde toda sua energia (potencial e cinética) devido à força de atrito, logo, pela conservação da energia:
Resposta
a)
b)
c)
d)