Fundamentos de Física – Halliday e Resnick. 9° Ed. Volume 1. Seção 8.5, Questão 36.
(Cap. 8 – Ex. 5) Duas meninas estão disputando um jogo no qual tentham acertar uma pequena caixa no chão com uma bola de gude lançada por um canhãao de mola montado em uma mesa. A caixa está a uma distância horizontal da borda da mesa; veja a Fig. 8-46. Lia comprime a mola , mas o centro da bola de gude cai antes do centro da caixa. De quanto Rosa deve comprimir a mola para acertar a caixa? Suponha que o atrito da mola e da bola com o canhãao seja desprezível.
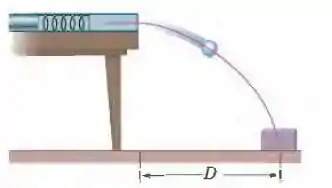
Figura 8-46 Problema 36
Passo 1
Fala aí pessoal!
Nessa questão, a gente tem uma situação em que uma bolinha é lançada de cima de uma mesa e ela se move pro lado e pra baixo. Isso quer dizer que é uma questão de lançamento oblíquo.
O lançamento oblíquo da bolinha pode ser estudado de 2 formas:s:
- na horizontal, temos movimento uniforme, então a função horária será .
- Nnao vertical, temos movimento uniformemente variado provocado pela gravidade, com sua função horária dada por
. Tomando como referencial o topo da mesa e para baixo como positivo para y, temos Então, das equações ali de cima, temos:
Isolando em , temos
Substituindo em
Dessa equação, podemos notar que a distância em é proporcional a velocidade inicial do movimento. E, e sendo a distância percorrida pela bolinha (), temos
Onde representa uma constante qualquer
Supondo que o 2° lançamento atinja a distância , temos
Passo 2
A energia cinética no instante do lançamento deve ser igual a energia potencial elástica no início do movimento (lei da conservação da energia). Então
Dessa forma, nota-se que a velocidade inicial do lançamento é proporcional à compressão da mola
Pode-se então retirar uma relação dos 2 lançamentos em função da velocidade inicial e da variação de comprimento da mola
Passo 3
Combinando as equações encontradas
Para , e .