Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de círculos, hipérboles e parábolas

Ver Teoria
Exercício 123456789

Enunciado

Esboce o gráfico da função:

j x = x 2 - 1    

Passo 1

Como sempre, vamos chamar o nosso j x   d e   y .

y = x 2 - 1

O diferente dessa questão é que para qualquer valor de x existirá resultado para essa raiz quadrada pois esse resultado será SEMPRE maior ou igual a zero.

Vamos ver para quais valores a nossa função é positiva e quais ela é negativa. Pois:

Para os valores de x ² - 1 positivos teremos que :

y = x 2 - 1

Já para os valores negativos de x ² - 1 teremos :

y = 1 - x ²

Passo 2

Fazendo o estudo do sinal, teremos:

x ² - 1 = x - 1 x + 1

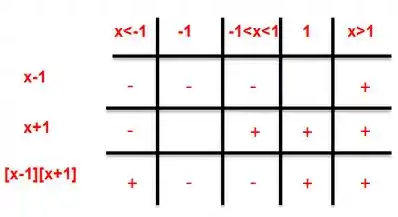
Logo, vemos que:

y = x 2 - 1   s e       x ≥ 1   o u   x < - 1       [ I ]

y = 1 - x ²     s e         - 1 ≤ x < 1         [ I I ]

Passo 3

Resolvendo a equação para o intervalo [I], teremos:

y ² = x ² - 1

x 2 1 ² - y 2 1 2 = 1

Logo, a gente vê que para o intervalo [I] teremos uma hipérbole centrada em C = 0,0 e vértice V ' = 0 - 1 = - 1   e   V ' ' = 0 + 1 = 1 . Mas lembrando... Só para valores de y ≥ 0 por causa da raiz quadrada lá que só nos da valores positivos! :D

Agora resolvendo a equação para o intervalo [II], teremos:

y = 1 - x 2    

y 2 = 1 - x 2

x 2 + y ² = 1

Temos uma circunferência de raio R = 1 , centrada na origem. Logo o nosso gráfico será:

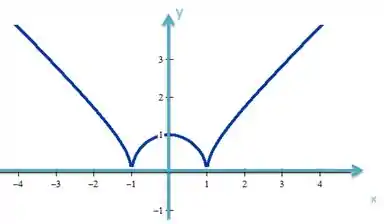
Resposta

Dada na resolução.