UFF, Cálculo IA-Lista 1, GMA, 2008-1, 40
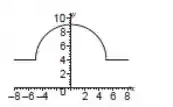
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
O esboço desse gráfico é mais simples do que você imagina. Observe que para ou a função é constante e vale . Então só precisaremos substituir valores no intervalo . O esboço fica assim:
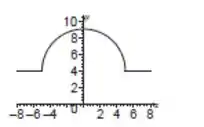
Passo 2
A função só pode ter restrições ao domínio no intervalo , que é onde possui uma raiz quadrada.
Olha que coisa boa! O intervalo em que essa raiz está definida é justamente o intervalo da função. Portanto, como no resto do domínio a função é constante, ele não possui restrições.
Quanto à imagem, pelo esboço do gráfico vemos que assume seu valor máximo na interseção com , ou seja, quando .
O valor mínimo é . Então
Passo 3
Só falta verificar a paridade da função.
Se :
Se :
Resposta
