UFF, Cálculo IA-Lista 1, GMA, 2008-1, 41
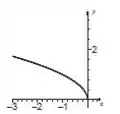
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
De cara já podemos ver que só poderá assumir valores negativos, caso contrário a raiz quadrada terá um valor negativo e isso não pode acontecer. Sabendo disso, basta substituir valores para ,como , , ..., e marcar no gráfico. O esboço fica desse jeito:
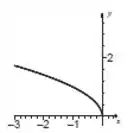
Passo 2
Vimos no Passo 1 que o domínio da função não pode ter valores de , pois a raiz ficaria negativa. Fora isso não há mais nenhuma restrição para , logo
Quanto à imagem, pelo esboço do gráfico vemos que o menor valor que a função assume é e que depois ela cresce infinitamente. Por isso
Passo 3
Resposta
