UFF, Cálculo IA-Lista 1, GMA, 2008-1, 36
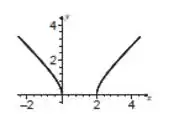
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
Para esboçar o gráfico dessa função iremos substituir valores e ir marcando no plano cartesiano. Comece olhando as interseções com os eixos e depois valores simples de , como , , e assim por diante, até você perceber que o comportamento da função não está mais se alterando. Não se esqueça de substituir valores negativos também. Feito isso, o esboço do gráfico fica assim:
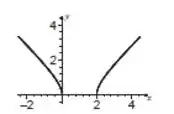
Passo 2
Como é uma função possui raiz quadrada temos que ver para quais valores ela fica negativa e, consequentemente, não está definida.
Ora, ora! Chegamos na equação de uma parábola de concavidade para cima cujas raízes são
Então entre e , isto é, a função é negativa. E quando ou a função é positiva. Portanto:
Quanto à imagem, pelo esboço do gráfico vemos que o menor valor que a função assume é e que depois ela cresce infinitamente. Por isso
Passo 3
Só falta verificar a paridade da função.
Resposta
