UFF, Cálculo IA-Lista 1, GMA, 2008-1, 37
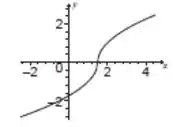
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
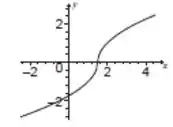
Para esboçar o gráfico dessa função não tem nenhum mistério, faremos do mesmo jeito das questões anteriores: substituindo valores. Só precisamos ficar ligados porque a partir de a lei de formação muda, então os valores serão substituídos na nova lei de formação. Fora isso o procedimento é o mesmo, achar interseções (se existirem), escolher valores de e marcar no plano cartesiano. Nesse caso o gráfico fica assim:
Passo 2
Como a função possui raízes quadradas temos que ver para quais valores elas ficam negativas.
Vish! Parece que chegamos a um dilema, porque para uma raiz o precisa ser menor que e para a outra precisa ser maior ou igual a . Na verdade, isso não será um problema pra gente, nesse caso, porque a função é definida por partes e cada raiz está inserida em um domínio diferente. A primeira só será usada se e a outra só se . Portanto, unindo esses dois domínios para obter o domínio da função inteira vemos que:
Quanto à imagem, pelo esboço do gráfico vemos que a função assume todos os valores de positivo e todos os valores de negativo. Por isso
Passo 3
Só falta verificar a paridade da função.
Se :
Se :
Resposta
