Esboce o gráfico da função:
Passo 1
Opa, temos uma função composta! Devemos analisar as duas partes da equação. Primeiro, claro, chamando o de teremos:
Na primeira parte:
Elevando os dois lados ao quadrado, teremos:
Mas toma cuidado na raiz, como sabemos, temos somente a parte positiva do gráfico, sendo o resultado da raiz quadrada sempre , logo:
Nosso gráfico será esboçado a partir da reta . :D
Passo 2
Ajeitando a nossa equação, teremos:
Isso é exatamente a equação da circunferência, que é dada por:
Logo, teremos uma circunferência centrada em e de raio .
Relembrando:
- Para valores acima da reta .
- No intervalo .
- Para o resto da reta, ou seja, no intervalo teremos .
Logo o nosso gráfico será:
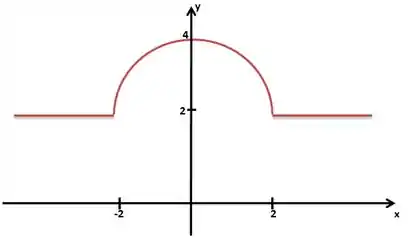
Resposta
Dada na resolução.