Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de círculos, hipérboles e parábolas

Ver Teoria
Exercício 512346789

Enunciado

UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 12

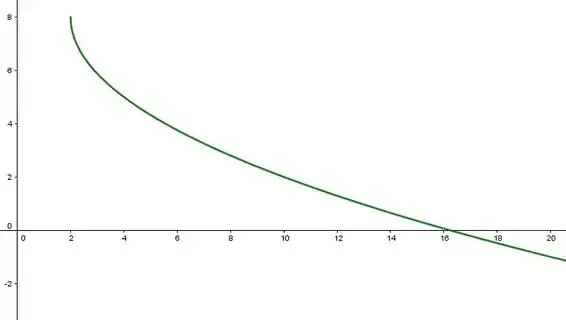
Esboce o gráfico da função abaixo

f x = 8 - 3 x 2 - 1

Passo 1

A primeira coisa a fazer é determinar o domínio da função.

A única restrição da função é a raiz quadrada, o termo dentro dela não pode ser negativo:

x 2 - 1 ≥ 0

x 2 ≥ 1

⇒ x ≥ 2

Show, então o domínio da função é 2 ,   ∞ .

Passo 2

Agora vamos entender melhor essa função. Por enquanto vou ignorar o 8 e focar na raiz quadrada, beleza? Temos:

y = - 3 x 2 - 1

Elevando ao quadrado, pra eliminar a raiz quadrada:

y 2 = 9 x 2 - 1

y 2 9 = x 2 - 1

x 2 = y 2 9 + 1

⇒ x = 2 9 y 2 + 2

Ótimo, essa é a equação de uma parábola!

Passo 3

Essa é uma parábola “deitada”, com equação

x = a y 2 + b y + c = 2 9 y 2 + 2

Ou seja, a = 2 9 e b = 0 e c = 2 .

Como a > 0 , a sua concavidade é voltada pra direita.

Passo 4

Agora vamos calcular as coordenadas m ,   n do vértice da parábola. Lembra lá da teoria?

a = 1 2 p = 2 9 , b = - n p = 0 , c = n 2 2 p + m = 2

Pela 2ª equação, temos que n = 0 . Substituindo na 3ª, dá m = 2 .

Então o vértice dessa parábola é o ponto 2 ,   0 .

Obs.: obtivemos uma parábola voltada pra direita, cuja coordenada x do vértice é 2 , isso condiz com o domínio da função que é x ≥ 2 .

Passo 5

Com essas informações já dá pra tirar um gráfico da parábola: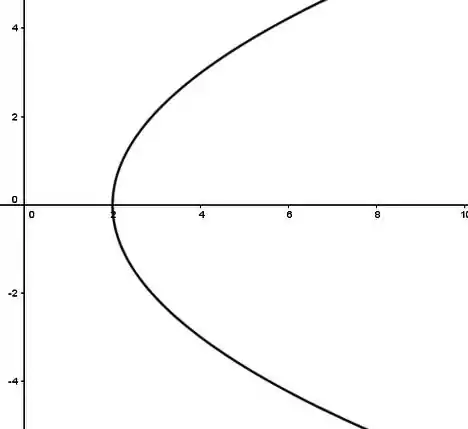

Só que atenção!! Inicialmente tínhamos y = - 3 x 2 - 1 , ou seja, y < 0 . Então na verdade o gráfico vai ser só a metade inferior da parábola (na hora que elevamos ao quadrado acabou dando a equação da parábola toda):

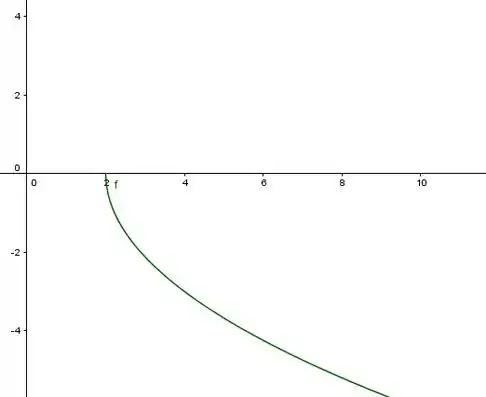
Passo 6

Mas isso tudo fizemos com y = - 3 x 2 - 1 . Mas a nossa função é f x = 8 - 3 x 2 - 1 , então basta pegar esse gráfico que obtivemos e deslocar ele 8 pra cima! Aí fica:

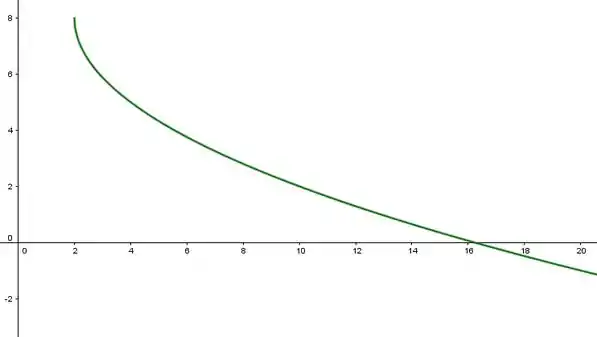
Resposta