Nos exercícios 27 e 28 verifique que as equações são do tipo Clairaut e encontre uma família de soluções e as soluções singulares na forma paramétrica. [lembrando, tipo Clairaut: ]
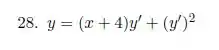
Nos exercícios 27 e 28 verifique que as equações são do tipo Clairaut e encontre uma família de soluções e as soluções singulares na forma paramétrica. [lembrando, tipo Clairaut: ]
Passo 1
Bom, então a primeira coisa é verificar se nossa EDO é de Clairaut ou não. Olha ela aqui:
Olha que linda, já esta no formato certinho! Então beleza.
Passo 2
Agora o que a gente faz é derivar em ambos os lados com respeito a :
Isso nos diz que:
Passo 3
Vamos então estudar os dois casos. Se:
Substituindo isso na EDO:
Agora se:
Adotando e substituindo na EDO:
Resposta
Família de soluções: . Solução singular:
Exercícios de Livros Relacionados
Mostre que 8 é uma solução para 7 . Sugestão: Derive ambos as lados de 7 com relação a x e considere dois casos. Use a diferenciação paramétrica para mostrar: d y d x = d y d t d x d t = t ,f ' ' ( t
Nos problemas 19-24, resolva a equação de Clairaut dada. Obtenha uma solução singular.23. x y ' - y = e y '
Quando R x = - 1 , a equação de Ricatti pode ser escrita como y ' + y 2 - Q x y - P x = 0 . Mostre que a substituição y = w ' w conduz à equação linear de segunda ordem w ' ' - Q x w ' - P w w = 0 (Qu
Nos problemas 19-24, resolva a equação de Clairaut dada. Obtenha uma solução singular.21. y = x . d y d x - d y d x 3
Nos problemas 19-24, resolva a equação de Clairaut dada. Obtenha uma solução singular.19. y = x y ' + 1 - ln y '