Uma avançada turbina chamada de ventilador não canalizado (UDF) é uma das novas tecnologias mais promissoras que tem sido desenvolvida para o futuro transporte de aeronaves.
Turbinas, que têm sido usadas por décadas, combinam o poder e a confiabilidade dos motores a jato com a eficiência dos propulsores. Eles constituem uma importante melhoria dos antigos propulsores movidos a pistão. Suas aplicações têm sido limitadas a pequenas aeronaves do tipo comutador, isto porque eles não são tão rápidos, nem poderosos quanto as turbinas usadas em grandes aeronaves. Esse tipo de turbina (UDF) implica em avanços significantes na tecnologia de propulsão. Novos materiais, aerodinâmica e velocidades de alta rotação habilitam esta turbina a voar tão rápido quanto as turbinas a jato, e com grande aproveitamento de combustível. A UDF é também menos barulhenta que o sistema convencional de turbinas.
Durante um teste de vôo de uma turbina UDF de uma aeronave, o motor é levado para um nível de , o que significa os da aeronave tendo alcançado uma velocidade de . As válvulas de regulação do motor são então levadas para atingir um nível de , e a aeronave começa a acelerar.
A equação diferencial que determina a aceleração da aeronave é:
Onde:
nível atingido em
massa em
velocidade em
Escreva no MATLAB um programa para determinar a nova velocidade depois de uma mudança no nível do motor através do gráfico da solução para a equação diferencial. Considere um intervalo de tempo de 6 min.
Passo 1
O enunciado nos dá a seguinte EDO de primeira ordem:
Substituindo por , que é o valor da massa da aeronave, temos a EDO:
Onde é o nível do motor em , o tempo em é a variável independente e , a velocidade da aeronave em , é a função que queremos descobrir resolvendo a EDO.
O enunciado diz que quando o nível do motor é , a aeronave atinge uma velocidade de . Em seguida, o nível do motor sobe para . Ao final, nos é perguntado qual é a velocidade da aeronave com o motor atinge um nível de . Para encontrar esta velocidade, temos que considerar na EDO acima. Logo, a EDO que temos que encontrar uam solução é:
De maneira indireta, o enunciado nos dá o intervalo de integração e a condição inicial para resolver a EDO.
O enunciado nos diz pra considerarmos um intervalo de 6 min. Considerando o instante inicial de e o final , temos que o intervalo de integração é .
O enunciado diz que a aeronave tem uma velocidade de quando o nível do motor vai para . Logo, a condição inicial é .
Portanto, temos todas as entradas necessárias para usar a função do MATLAB.
Além disso, o exercício pede para mostrarmos no gráfico da solução da EDO a velocidade que a aeronave atinge quando o nível do motor é . Por isso, no final, também teremos que gerar um gráfico de considerando .
Passo 2
Primeiramente, vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a seguinte estrutura:
Ela exige três entradas, fornecidas pelo enunciado:
- : uma função representando a EDO de primeira ordem:
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, e , logo, ;
- : condição inicial de em . Neste exercício, .
E ela nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração . Usaremos os vetores e para gerar o gráfico pedido.
Depois de relembrar a função , vamos abrir um script novo no MATLAB para criarmos uma função com a EDO do enunciado. Nesse script, digite as linhas de código:
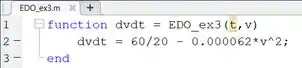
Após criar a função , abra um novo script para implementar a função . Neste script, digite as linhas de código:

Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: ’. Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de .
Passo 3
Com os códigos do passo 2, encontramos a solução da EDO. Mas falta ainda uma coisinha: gerar o gráfico de . Para isto, usaremos a saída de os vetores e .
No mesmo script onde você implementou , digite as linhas de código:

A primeira linha gera o gráfico da velocidade em função do tempo.
A segunda linha dá um nome para o eixo horizontal do gráfico, usando a função . Foi dado um nome de .
A terceira linha dá um nome para o eixo vertical do gráfico, usando a função . Foi dado um nome de .
Ao rodar o programa, o gráfico de tempo versus velocidade é gerado e nele podemos encontrar a resposta do exercício:

Repare que a curva se estabiliza em torno de . Isto quer dizer que a nova velocidade da aeronave depois de uma mudança no nível do motor de para é .
Resposta
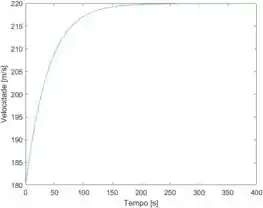
A nova velocidade da aeronave depois de uma mudança no nível do motor de para é .