Considere o reator bioquímico descrito na figura abaixo, onde representa a biomassa presente no reator e o substrato. O reator possui um volume constante () uma vez que as vazões de alimentação e de saída são iguais (). A corrente de alimentação possui concentração de substrato igual a x2i e uma concentração de biomassa igual a zero.
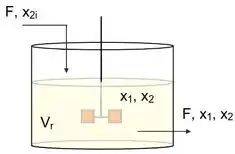
Bequette (1998) propõe o modelo descrito pela equação abaixo para o processo:
onde é a relação constante entre as taxas de geração de biomassa e o consumo de substrato e é o coeficiente de taxa de crescimento descrito pela equação:
Descreva o comportamento das concentrações de biomassa e de substrato considerando um tempo de integração de 30 horas (), as condições iniciais:
E os valores para os parâmetros descritos na tabela abaixo:

BEQUETTE, B. W., Process Dynamics: Modeling, Analysis and Simulation, 1a ed. USA, PrenticeHall PTR, 1998.
Passo 1
O exercício nos dá um sistema de EDOs de primeira ordem, composto de duas EDOs, representando as concentrações de biomassa () e de substrato () presentes em um reator bioquímico.
O enunciado pede para resolvermos o sistema de EDOs em um intervalo de integração de a horas, isto é, o intervalo de integração é .
Para resolvermos o sistema de EDOs, temos como condições iniciais:
Portanto, temos todas as entradas para usarmos a função do MATLAB para encontrarmos a solução do sistema de EDOs.
O exercício pede para descrevermos o comportamento das concentrações de biomassa e de substrato, isto é, de e , respectivamente, no intervalo de horas. Por isso, é legal no final gerarmos um gráfico com as curvas de e , plotadas usando o resultado da .
Passo 2
Vamos começar relembrando a função do MATLAB, que tem a estrutura:
Ela tem três entradas:
- : uma função representando o sistema de EDOs de primeira ordem, no caso:
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, , , logo ;
- : vetor com as condições iniciais de e em . Temos que , logo, .
A função nos dará duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e uma matriz de duas colunas com os valores de e (iniciando em e terminando nos valores de e correspondentes a ), representando a solução do sistema de EDOs. A primeira coluna de corresponde a e a segunda coluna de corresponde a .
Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam de e para o intervalo de integração .
Vamos implementar tudo isso no MATLAB. Primeiramente, abra um script novo e crie a função . Vamos entrar com os dados da tabela do enunciado, com as seguintes linhas de código:

Como queremos encontrar duas funções ( e ), a entrada da função é um vetor de dois elementos, o primeiro elemento representando e o segundo elemento, . A saídade é um vetor representando as derivadas das funções e e também é um vetor de dois elementos.
Em seguida, entre com a equação do coeficiente de taxa de crescimento:
Digitando a linha de código:
![]()
Tendo entrado com a equação de , finalmente podemos entrar com o sistema de EDOs:
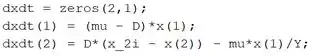
No final, a função ficou com essa carinha:

Passo 3
Após concluir a função , vamos resolver o sistema de EDOs. Digite os seguintes comandos em um novo script do MATLAB:

A primeira linha cria o intervalo de integração .
A segunda linha cria as condições iniciais de e . Elas são representadas por um vetor de dois elementos, .
Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string . Essa string é o nome da função criada para representar o sistema de EDOs.
A saída de será um vetor , representando a variável independente, e uma matriz com duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs.
Passo 4
O exercício pede para analisarmos o comportamento das concentrações de biomassa e de substrato, isto é, de e , respectivamente, no intervalo de horas. Por isso, vamos gerar um gráfico com as curvas de e , usando os vetores de saída e da .
Para plotar e , entre os seguintes comandos no script onde você usou a função :

Na primeira linha, usamos a função para gerar, em um mesmo gráfico, as curvas de e . O primeiro par pega a primeira coluna de , correspondendo a e a plota em função de . Da mesma maneira, o segundo par pega a segunda coluna de , correspondendo a e a plota em função de .
Na segunda linha, acrescentamos uma legenda ao gráfico, indicando que o par representa a concentração de biomassa e o par representa a concentração de substrato.
Na terceira linha, damos um nome para o eixo horizontal do gráfico usando o comando . O nome indica que no eixo horizontal temos o tempo em horas.
Na quarta linha, damos um nome para o eixo vertical do gráfico usando o comando . O nome indica que no eixo vertical temos a concentração em gramas/litro.
Rodando o programa, o gráfico será gerado e podemos analisar o comportamento da biomassa e do substrato.
Resposta
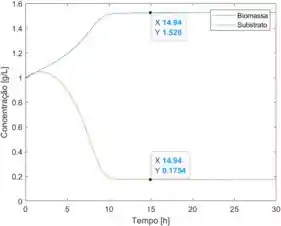
O gráfico acima contém as curvas de concentração de biomassa (, em azul) e de substrato (, em vermelho), em um reator bioquímico, para um intervalo de a horas.
No começo, nas primeiras horas, a concentração de biomassa aumenta, enquanto a de substrato diminui. Após as primeiras horas, as concentrações de biomassa e substrato se estabilizam e tornam-se constantes.