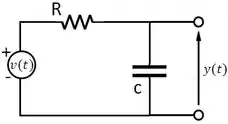
O modelo do circuito RC mostrado na figura abaixo pode ser encontrado a partir da lei das tensões de Kirchhoff e da conservação da carga:
Suponha que o valor de seja . Utilize um método numérico para encontrar a resposta para o caso em que a tensão externa aplicada é zero e que a tensão inicial do capacitor seja . Compare os resultados com a solução analítica, que é
Passo 1
O exercício nos dá uma EDO que modela um cicuito RC e uma condição inicial, e nos pede para encontrar a solução da EDO , que representa a tensão do capacitor. O enunciado não nos dá um intervalo de integração, representando o tempo , mas podemos escolher um intervalo qualquer. Uma EDO, uma condição inicial e um intervalo de integração são as três entradas da função do MATLAB, que resolve EDOs de primeira ordem usando métodos de Runge-Kutta. Logo, usaremos essa função para encontrar .
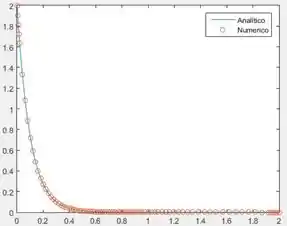
Em seguida, ele nos pede para compararmos a solução encontrada com , isto é, a solução numérica da EDO, à solução analítica. Para isto, geraremos um gráfico com duas curvas: uma representando a solução obtida por e a outra representando a solução analítica.
Passo 2
Primeiramente, vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a sintaxe:
Ela exige três entradas:
- : uma função representando a EDO de primeira ordem . Neste exercício, é a EDO ;
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . O enunciado não especificou o intervalo de integração, por isso podemos escolher o intervalo que quisermos. Vamos adotar e , logo, ;
- : condição inicial de em . Neste exercício, .
A função nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração . Usaremos os vetores e para gerar o gráfico comparando a solução numérica com a solução analítica.
Vamos começar pela função representando a EDO. O primeiro passo é reorganizar os termos a EDO do enunciado, de forma que a derivada fique isolada no lado esquerdo da EDO. Lembrando que :
Agora podemos passar a EDO para o MATLAB. Crie um script novo e digite as linhas de código:

Com estas linhas de código, é criada a função , representando a EDO do enunciado. Ela recebe valores de e e retorna a derivada .
Passo 3
Após criar a função , abra um novo script para implementar a função . Lembre de salvá-lo na mesma pasta onde você salvou a função . Neste script, digite as linhas de código:

Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: . Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de . Esses vetores representam a solução numérica da EDO, a qual plotamos a partir deles.
Passo 4
O exercício pede para compararmos a solução numérica da EDO com a solução analítica, dada por:
Vamos compará-las por meio de um gráfico. A primeira coisa a fazer é gerar valores de da solução analítica para plotar sua curva. Para isto, no mesmo script onde você implementou , digite a linha de código:
![]()
Esta linha de código é a função . Ela usa o vetor gerado pela e calcula a solução analítica para cada elemento de . Os resultados são armazenados no vetor .
Passo 5
Para gerar o gráfico comparando a solução analítica com a numérica, entre os comandos:
![]()
Na primeira linha, é usado o para gerar as curvas da solução analítica e da solução numérica. O primeiro par plota a solução analítica em função de . O segundo par plota a solução numérica em função de , e pede que a curva gerada seja composta por bolinhas ().
Na segunda linha, é adicionada uma legenda ao gráfico, para sabermos qual curva é qual. A legenda corresponde ao primeiro par e a legenda , ao segundo par .
Execute o programa e você terá o gráfico que permite comparar as duas soluções.
Resposta