Utilize um método de Runge-Kutta explícito para aproximar , sabendo que
![]()
Passo 1
O exercício nos dá uma EDO de primeira ordem e uma condição inicial: . Ele pede para encontrarmos usando um método de Runge-Kutta explícito.
Para encontrarmos , precisamos solucionar a EDO para encontrar . Como o exercício pede para usarmos um método de Runge-Kutta explícito, podemos usar a função do MATLAB, que resolve EDOs de primeira ordem usando um método explícito de Runge-Kutta.
Como temos uma condição inicial em () e o exercício pede para encontrarmos , temos que e nosso intervalo de integração vai ser .
Resumindo, neste exercício, usaremos a função para resolver a EDO e então encontrar .
Passo 2
A primeira coisa que devemos fazer é rearranjar os termos da EDO do enunciado:
Para que ela fique no formato:
Reorganizando os termos, temos:
É a EDO neste formato que usaremos na função do MATLAB.
Passo 3
Vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a seguinte estrutura:
Ela exige três entradas:
- : uma função representando a EDO de primeira ordem . Neste exercício, é a EDO ;
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, e , logo, ;
- : condição inicial de em . Neste exercício, .
A fnção nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração .
Crie um script novo no MATLAB para criarmos uma função com a EDO do enunciado. Nesse script, digite as linhas de código:
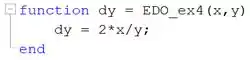
Com estas linhas de código, é criada a função , representando a EDO do enunciado. Ela recebe valores de e e retorna a derivada .
Após criar a função , abra um novo script para implementar a função . Neste script, digite as linhas de código:

Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: ’. Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de .
Passo 4
Para encontrarmos , temos que olhar o último elemento do vetor , pois ele corresponde ao valor da função no final do intervalo .
No mesmo script onde implementamos a função , vamos adicionar o comando:
![]()
Com este comando, o último elemento do vetor , indicado pelo índice , é armazenado na variável . Portanto, , que é a resposta do exercício.
Rodando o programa, temos:
