Seja a equação:
- Assumindo como condição inicial , resolva, no MATLAB, essa equação diferencial no intervalo de e plote o gráfico com os valores correspondentes de .
- Sendo a solução analítica para esta equação, faça um novo gráfico que compare a solução analítica com a numérica.
Passo 1
O exercício nos dá uma EDO, uma condição inicial e um intervalo e nos pede para encontrar a solução da EDO . Essas são as três entradas da função do MATLAB, que resolve EDO de primeira ordem usando métodos de Runge-Kutta.
Em seguida, ele nos pede para gerarmos um gráfico de . As saídas da função são valores de e , representando a solução da EDO. Essas saídas podem ser usadas para plotar o gráfico de .
Portanto, usaremos para resolver a letra a do exercício.
A letra b dá a solução analítica da EDO e pede para gerar um novo gráfico comparando as curvas da solução analítica e da solução numérica, isto é, a solução obtida usando na letra a.
Passo 2
Primeiramente, vamos relembrar a função , para vermos o que entraremos no MATLAB. A função possui a seguinte estrutura:
Ela exige três entradas:
- : uma função representando a EDO de primeira ordem . Neste exercício, é a EDO ;
- : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, e , logo, ;
- : condição inicial de em . Neste exercício, .
E ela nos dá duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e outro com os valores de (iniciando em e terminando no valor de correspondente a ), representando a solução da EDO. Em outras palavras, 𝑜𝑑𝑒45 nos retorna os pontos que representam a função para o intervalo de integração . Usaremos os vetores e para gerar o gráfico pedido na letra a.
Agora, crie um script novo no MATLAB para criarmos uma função com a EDO do enunciado. Nesse script, digite as linhas de código:
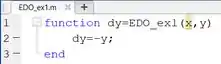
Com estas linhas de código, é criada a função , representando a EDO do enunciado. Ela recebe valores de e e retorna a derivada .
Após criar a função , abra um novo script para implementar a função . Neste script, digite as linhas de código:

Na primeira linha, entramos com o intervalo de integração .
Na segunda linha, entramos com o valor inicial .
Na terceira linha, entramos com a função para encontrar uma solução da EDO. Repare que, no lugar de 𝐸𝐷𝑂_𝑓𝑢𝑛, coloquei um string com o nome da função que representa a EDO: ’. Não esqueça de pôr o nome entre aspas simples, como no print acima.
A solução da EDO é dada pelos vetores e , saídas de .
Passo 3
Com os códigos do passo 2, encontramos a solução da EDO. Mas falta ainda uma coisinha: gerar o gráfico de . Para isto, usaremos a saída de os vetores e .
No mesmo script onde você implementou , digite as linhas de código:
![]()
Na primeira linha, pedimos ao MATLAB para criar uma figura de índice 1. Fazemos isso já prevendo que mais para frente plotaremos outro gráfico, para a letra b do exercício, e quermos que estes gráficos sejam gerados em janelas diferentes.
O comando na segunda linha efetivamente gera o gráfico da solução da EDO.
Rode seu programa e você terá este lindo gráfico:
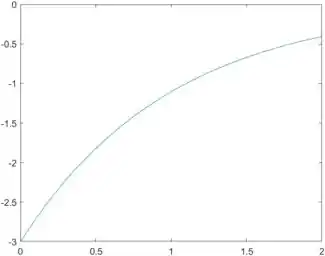
Pronto! Letra a respondida ;)
Passo 4
Vamos responder à letra b do exercício. Ela nos diz que a solução analítica de é:
E pede para gerarmos um gráfico comparando a solução analítica com a numérica, obtida na letra a.
A primeira coisa a fazer é gerar valores de da solução analítica para plotar a curva. Para isto, no mesmo script onde você resolveu a letra a, digite a linha de código:
![]()
Esta linha de código é a função . Ela usa o vetor gerado pela e calcula a solução analítica para cada elemento de . Os resultados são armazenados no vetor .
Em seguida, para gerar o gráfico comparando a solução analítica com a numérica, entre os comandos:
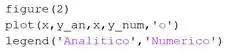
Na primeira linha, pedimos ao MATLAB para gerar uma figura com índice 2. Este comando serve para gerar os gráficos das letras a e b em janelas diferentes.
Na segunda linha, é usado o para gerar as curvas da solução analítica e da solução numérica. O primeiro par plota a solução analítica em função de . O segundo par plota a solução numérica em função de , e pede que a curva gerada seja composta por bolinhas ().
Na terceira linha, é adicionada uma legenda ao gráfico, para sabermos qual curva é qual. A legenda corresponde ao primeiro par e a legenda , ao segundo par .
Basta rodar o programa que você terá a solução da letra b :)
Resposta
A curva azul representa a solução analítica e a curva composta por círculos vermelhos corresponde à solução numérica.