A equação de movimento para um pêndulo cuja base se move horizontalmente com uma aceleração é

Suponha , e . Plote para para os seguintes casos:

1. aceleração constante e ou
2. aceleração linear com o tempo e

Antes de partir para o MATLAB, temos que converter a EDO de segunda ordem para um sistema de EDOs de primeira ordem. Para isto, vamos dizer que:

Substituindo e na EDO original, temos:

Isolando na equação acima, temos:

Esta é a primeira equação do sistema de EDOs de primeira ordem.

Para construir a segunda equação do sistema, considere que:

Logo, o sistema de EDOs de primeira ordem construído a partir de é:

Usaremos esse sistema para resolver a letra a e a letra b do exercício.

Com o sistema de EDOs de primeira ordem, podemos partir para o MATLAB. Vamos começar respondendo a letra a, que pede para plotarmos para para aceleração constante e duas consições iniciais distintas: e . Para isto, usaremos a função do MATLAB, que tem a estrutura:

Ela tem três entradas:

• : uma função representando o sistema de EDOs de primeira ordem, no caso:
• : intervalo de integração, normalmente no formato : o intervalo começa em e termina em . Neste exercício, , , logo ;
• : vetor com as condições iniciais de e em .

Temos que e duas condições iniciais para : e . Por isso, vamos implementar 𝑜𝑑𝑒 para dois diferentes na letra a: e .

Para ambos os casos, a função nos dará duas saídas: um vetor com valores de (começando em e terminando em , correspondendo ao nosso intervalo de integração) e uma matriz de duas colunas com os valores de e (iniciando em e terminando nos valores de e correspondentes a ), representando a solução do sistema de EDOs. A primeira coluna de corresponde a , isto é, a , e a segunda coluna de corresponde a , ou seja, .

Em outras palavras, 𝑜𝑑𝑒 nos retorna os pontos que representam a função , na forma de para o intervalo de integração . Logo, é a segunda coluna de que vamos plotar.

Bora implementar tudo isso no MATLAB. Abra um script novo e crie a função , com o sistema de EDOs obtido no passo anterior:

Como queremos encontrar duas funções ( e ), a entrada da função é um vetor de dois elementos, o primeiro elemento representando e o segundo elemento, . O vetor representando as derivadas das funções e , , também é um vetor de dois elementos.

Note que a função serve para resolver a letra a do exercício, pois adotamos a aceleração constante .

Para resolver o sistema de EDOs para as duas condições iniciais da letra a, digite os seguintes comandos em um novo script do MATLAB:

A primeira linha cria o intervalo de integração .

As duas linhas seguintes se referem à condição inicial e as duas últimas linhas, a .

A segunda linha cria as condições iniciais de e para . Elas são representadas por um vetor de dois elementos, .

Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string . Essa string é o nome da função criada para representar o sistema de EDOs.

A saída de para será um vetor , representando a variável independente, e uma matriz com duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs para .

De maneira similar, a quarta linha cria as condições iniciais de e para , indicadas por .

A linha seguinte usa para resolver o sistema para . As saídas serão um vetor e uma matriz de duas colunas, a primeira representando e a segunda, . A saída representa a solução do sistema de EDOs para .

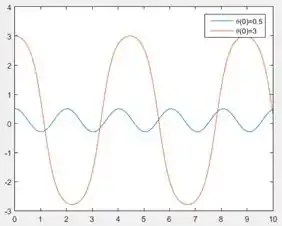
Após obtermos a solução do sistema EDOs para ambas as condiçõe inicias da letra a, podemos gerar as curvas de para ambos os casos, usando as saídas de . A 𝑜𝑑𝑒45 nos retorna os pontos que representam na primeira coluna de e e os pontos que representam na segunda coluna de e . Sabendo que e é que o exercício nos pede para plotar, são as segundas colunas de e que usaremos para plotar o gráfico.

Para plotar para uma acelerção constante com as duas condições iniciais distintas, entre os seguintes comandos no script onde você usou a função :

Na primeira linha, pedimos ao MATLAB para gerar um figura com o comando . Esta figura terá o gráfico de da letra a do exercício. Usamos esse comando para que os gráficos da letra a e b seja plotados em janelas diferentes.

Na segunda linha, usamos a função para gerar, em um mesmo gráfico, as curvas de para e . O primeiro par se refere a e pega a segunda coluna de , correspondendo a , e a plota em função de . Da mesma maneira, o segundo par é referente a e pega a segunda coluna de , também correspondendo a , e a plota em função de .

Na terceira linha, acrescentamos uma legenda ao gráfico, indicando que o par se refere a a e o par se refere a a .

Para obter o gráfico da letra a, rode o programa:

A letra b pede para plotar considerando uma aceleração linear com o tempo e . Para isto, também usaremos a função para resolver o sistema de EDOs de primeira ordem do passo 2, mas devemos montar uma nova função com o sistema de EDOs, considerando que varia com o tempo. Por isso, em um novo script, copie e cole a função criada no passo 3, alterando a variável para :

Chamei essa nova função de . Ele tem exatamente a mesma forma da anterior, a única diferença é que a variável não é mais constante.

Após salvar a função , no mesmo script onde você resolveu a letra a do exercício, implemente mais uma vez, mas para :

A primeira linha cria as condições iniciais de e para . Elas são representadas por um vetor de dois elementos, .

Em seguida, usamos a para resolver o sistema. Repare que no lugar de coloquei uma string , para resolver o sistema de EDOS com as condições da letra b. A saída de para a letra b do exercício será o vetor , representando a variável independente, e a matriz de duas colunas , a primeira representando e a segunda, .

Como , é a segunda coluna de que vamos plotar.

Para plotar para a letra b do exercício, adicione em seu script os comandos abaixo:

Na primeira linha, pedimos ao MATLAB para criar uma segunda figura, com o comando . Desta forma, teremos os gráficos da letra a e da letra b em janelas diferentes.

Na segunda linha, usamos o comando para plotar com aceleração linear com o tempo. Para isto, plotamos o par , que plota a segunda coluna de em função de .

Rode o programa e você terá o gráfico da solução da letra b do exercício.