(Adaptado) Uma superfície quadrada de de lado está posta sobre uma circuito gerador de energia térmica que mantém a superfície referida a . Essa superfície possui sobre ela um conjunto de pinos circulares.
São 25 pinos dispostos em 5 fileiras de 5 pinos. Os pinos possuem de diâmetro, de comprimento e estão distribuídos uniformemente a partir de um pino central localizado no centro da placa e espaçados igualmente de (distância entre as fileiras e os pinos da mesma fileira).
Existe um escoamento externo com ar a que escoa perpendicularmente a esse conjunto de pinos a uma velocidade de .
Determine a perda de calor do sistema e diga se o sistema foi bem dimensionado ou não, justificando sua resposta.
As propriedades termofísicas do ar são consideradas constantes e dadas pelo valor delas a .
Passo 1
Antes de qualquer coisa, vamos determinar as propriedades do ar. De acordo com a tabela A.4, para o ar a , temos:
Para a temperatura de superfície , temos .
Passo 2
A taxa de transferência de calor é dada por:
Dessa equação, nos temos praticamente tudo, menos o coeficiente convectivo médio e a temperatura de saída , que vamos precisar pra calcular a média logarítmica das temperaturas.
A temperatura de saída é dada por:
Arrumando essa equação, vamos encontrar o seguinte:
Não tem pra onde correr, vamos ter que ir atrás do coeficiente convectivo médio.
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Nesse caso, o problema nos deu que a distância entre os tubos é de e que o diâmetro dos tubos é de .
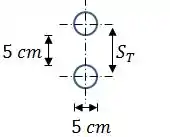
Dessa forma, os passos serão ambos iguais a . Logo:
Para esse valor de número de Reynolds, temos que:
Além disso, como , de acordo com a tabela na Teoria . Logo, o número de Nusselt será:
Passo 4
O coeficiente convectivo será dado por:
Voltando à expressão da temperatura de saída.
Substituindo os valores:
Passo 5
Voltando à expressão da taxa de transferência de calor por unidade de comprimento, temos:
Onde a média logarítmica de temperaturas é dada por:
Substituindo os valores:
![]()