Considere o escoamento de ar sobre um feixe de tubos alinhados, de acordo com a figura.
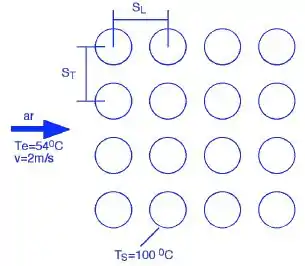
Dentro dos tubos escoa vapor d’água, a temperatura de . Os tubos têm diâmetro igual a e comprimento de . A distância entre os centros dos tubos vale . O ar entra a e . Sabe-se que o número de tubos na direção do escoamento é igual ao na direção transversal . Determine o menor número de tubos necessários para que a temperatura de saída do ar seja maior do que . Calcule a taxa de transferência de calor trocado entre o ar e os tubos. Despreze a resistência a condução nos tubos (i.e., considere que a temperatura na parede é igual a temperatura do vapor).
Passo 1
A primeira coisa que temos que fazer é determinar as propriedades do ar.
Como temos a temperatura de entrada e saída, vamos determinar as propriedades do fluido à temperatura média entre as duas. Assim:
Aproximando essa temperatura para , de acordo coma tabela A.4 do Incropera:
Já a , de acordo com a tabela A.4 do Incropera:
Obs.: Os dados foram obtidos através de interpolações, feitas diretamente na calculadora.
Passo 2
A temperatura de saída pode ser obtida através dessa expressão:
Onde . Assim, reorganizando a expressão acima, isolando , teremos:
Daqui, temos basicamente tudo, exceto o coeficiente convectivo. Então vamos calcula-lo!
Passo 3
O número de Nusselt, dado por:
Como a matriz possui uma configuração alinhada:
Para esse valor de número de Reynolds, temos que:
Além disso, supondo . O número de Nusselt será:
Passo 4
O coeficiente convectivo será, finalmente:
Voltando à expressão de :
Substituindo os valores:
Como é um número inteiro, o valor mínimo de será:
Finalmente, o número total de tubos será:
![]()
Passo 5
A taxa de transferência de calor será dada por:
Onde vale:
Substituindo os valores:
![]()