A barra da figura está engastada e sujeita ao carregamento mostrado abaixo, usando seus conhecimentos sobre esforços internos em vigas, determine as equações do cortante e do momento fletor para cada um dos trechos da barra.
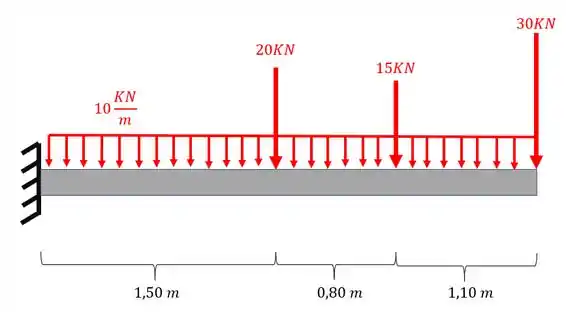
Passo 1
Sabemos que o nosso passo a passo para solucionar exercícios de diagrama de cortantes e momentos fletores seguem 4 passos
Primeiro fazemos o diagrama de corpo livre e determinamos as reações de apoio
Em segundo lugar dividimos a barra para calcularmos as equações
Em terceiro calculamos as equações
E por fim o quarto passo é determinar o nosso diagrama.
Como nesse caso a única coisa que é pedida são as equações, iremos apenas até o terceiro passo.
Mas uma pergunta que você pode se fazer é, quantas equações devemos fazer?
Para saber isso você analisa pontos em que ocorrem mudanças de carregamento, olhando a nossa figura teremos que
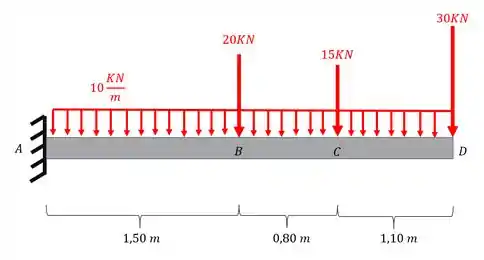
No trecho AB temos um carregamento constante, mas em B temos uma carga concentrada, logo temos uma mudança entre os trechos AB e BC, e no ponto C também temos uma carga concentrada, logo entre BC e CD também temos uma mudança.
Logo teremos uma equação entre AB, entre BC e entre CD. Ao todo então serão 3 equações.
Passo 2
Vamos lá então, como vimos o primeiro passo é determinar o diagrama de corpo livre e as reações de apoio, olhando a nossa barra teremos que
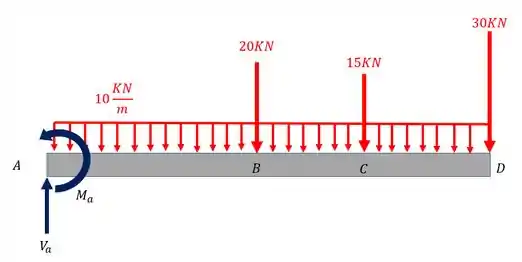
Logo teremos que
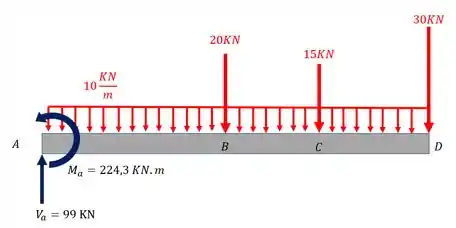
Passo 3
Agora precisamos cortar cada trecho da nossa peça, lembrar da nossa utilização de sinais e fazer o equilíbrio da peça.
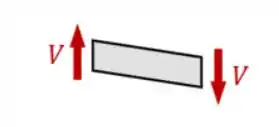
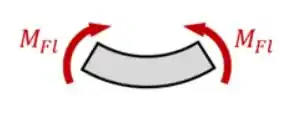
Os sinais analisados devem ser
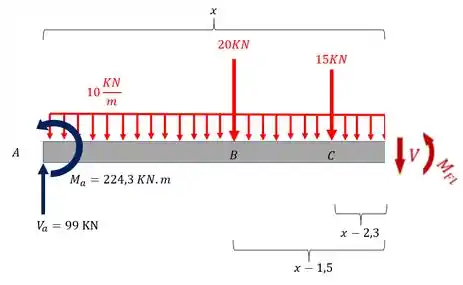
E cortando os trechos teremos
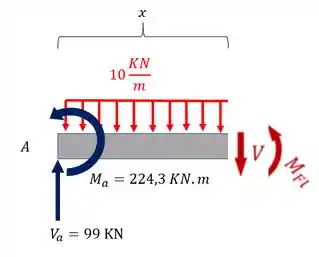
Para o trecho AB
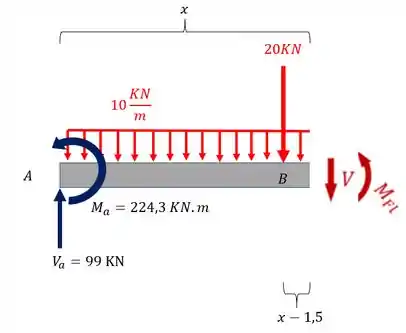
Para o trecho BC
Para o trecho CD
Passo 4
Agora vamos fazer o terceiro passo, que é exatamente fazer o equilíbrio da peça para calcular as equações.
Para o trecho AB teremos
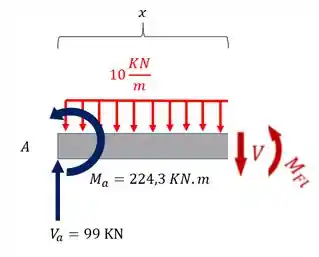
Para o cortante teremos que
E para o momento fletor teremos que
Para o trecho BC teremos
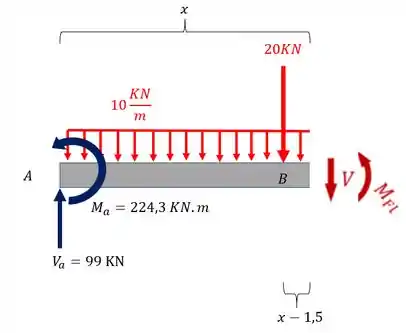
Para o cortante teremos que
E para o momento fletor teremos que
Para o trecho CD teremos
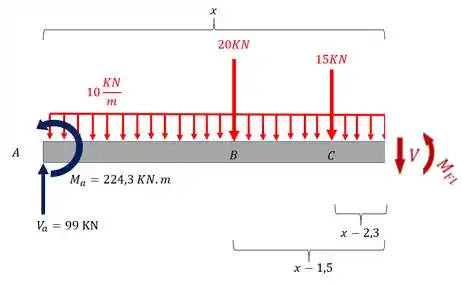
Para o cortante teremos que
E para o momento fletor teremos que