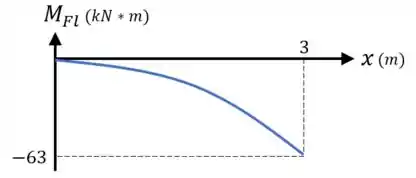
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
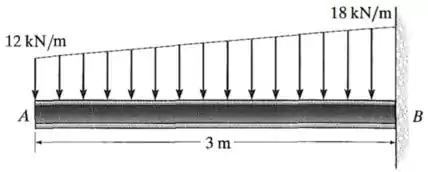
Passo 1
O exercício quer que a gente esboce os diagramas da força cortante e do momento fletor para a viga da figura.
Devemos resolver esses exercício da mesma forma que resolvemos outros exercícios parecidos:
- Fazendo um diagrama de corpo livre da viga;
- Aplicando as condições de equilíbrio na viga;
- Realizando uma análise dos esforços internos nela;
- E, finalmente, esboçando os diagramas de força cortante e momento fletor,
...mas dessa vez, temos a dificuldade adicional de lidar com essa força distribuída com o formato trapezoidal visto na imagem.
Então vamos começar pelo primeiro passo, que é o:
![]()
Nesse caso, tendo em mente:
- Que no engaste em , nós vamos ter uma reação na vertical , uma reação na horizontal e um momento ;
- E que, como não há nenhuma outra força horizontal nessa viga, a reação na horizontal vai ser nula/inexistente,
...o nosso DCL (diagrama de corpo livre) fica assim:
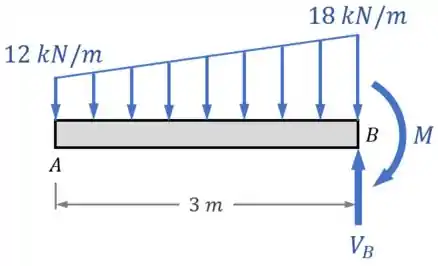
Passo 2
Feito o DCL, podemos seguir para o próximo passo que é o:
![]()
Aqui, podemos aplicar o equilíbrio de forças na horizontal e o equilíbrio de momentos em relação a um ponto.
Antes de fazer esses cálculos, é útil entender como a carga distribuída vai afetar a viga.
Para facilitar esse entendimento, podemos dividir a carga distribuída em duas cargas distribuídas menores:
A primeira vai ser constante, com valor de , e vai agir como uma força equivalente de bem no meio da viga.
A segunda vai ser triangular: ela vai variar linearmente entre e entre os pontos e .
Ela vai agir como uma força equivalente de:
...que vai estar localizada na centroide do triângulo, a do comprimento de da viga a partir do ponto .
Essas forças equivalentes estão representadas na figura abaixo, nas cores laranja e verde, respectivamente:
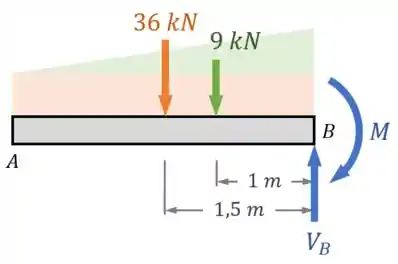
Tendo em mente essas forças equivalentes, podemos agora aplicar o equilíbrio de forças na horizontal:
Que nos diz que:
E o equilíbrio de momentos em relação ao ponto :
Que nos diz que:
Passo 3
Agora que conhecemos os esforços (forças e momentos) externos atuantes na viga, podemos seguir para a:
![]()
Para essa viga, só precisamos fazer uma seção para analisar os esforços internos ao longo de todo o comprimento de da viga.
(Isso porque essa viga só possui descontinuidades nas suas extremidades e .)
Fazendo essa seção, devemos ficar com um desenho semelhante ao desenho abaixo:
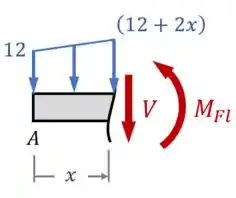
Observe como nesse desenho, tivemos que indicar uma equação que descrevesse o valor máximo da força dependendo da posição que queremos avaliar.
Para encontrar essa equação, podemos dizer que a força distribuída do exercício, que varia linearmente, é dada por uma função linear:
Aí, sabendo que a força distribuída tem o valor de para :
...encontramos que:
E sabendo que para , ela tem o valor de :
...encontramos que:
De tal forma que é dado por:
...ou , como está no desenho! :)
Agora...
Para terminar a análise, precisamos aplicar as condições de equilíbrio na viga secionada para encontrar o valor dos esforços internos e .
Mais uma vez, para aplicar essas condições de equilíbrio, é útil imaginar a força distribuída como duas forças distribuídas menores:
A primeira constante, igual à , que atua como uma força equivalente bem no meio dessa seção de viga de comprimento .
E a segunda triangular, igual à , que atua como uma força equivalente no centroide do triângulo, localizado à de distância da seção:
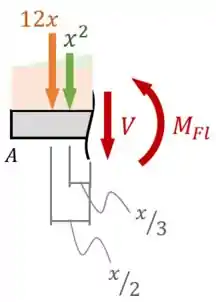
Com essas forças equivalentes em mente, conseguimos aplicar o equilíbrio de forças na vertical:
Que nos diz que:
E o equilíbrio de momentos em relação ao ponto da seção
Que nos diz que:
Passo 4
Por fim, chegamos ao último passo, que são os:
![]()
Para a força cortante , nós temos uma função quadrática :
- Com uma concavidade para baixo; (uma vez que a sua segunda derivada é negativa)
- E que varia de até .
Dessa forma, o seu diagrama fica assim:
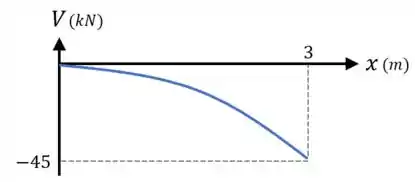
Já para o momento fletor , nós temos uma função de 3º grau :
- Com uma concavidade para baixo para valores de maiores que ; (uma vez que a sua segunda derivada é negativa para esses valores de )
- E que varia de até .
Sendo assim, vamos ter um o seguinte diagrama para o momento fletor: