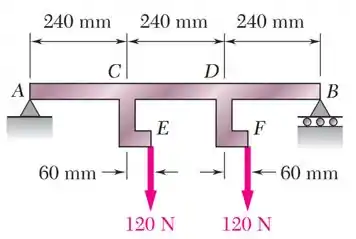
Trace os diagramas de força cortante e momento fletor para a viga e o carregamento mostrados na figura, e determine o valor máxima absoluto da força cortante e do momento fletor.
Passo 1
O exercício quer que a gente esboce os diagramas e determine os valores máximos da força cortante e do momento fletor na viga da figura.
Como sempre, começamos um exercício desse tipo fazendo o:

No caso desse exercício, temos que pensar o que as forças de nos pontos e vão gerar na viga principal .
Os pontos e estão conectados à viga pelos pontos e , então as forças de vão atuar nos pontos e da viga.
Mas como existe uma distância horizontal de entre os pontos e e entre os pontos e , as forças de também vão gerar um momento concentrado de...
...nos pontos e da nossa viga.
Tendo isso em mente, e sabendo:
- Que o apoio móvel em vai realizar somente uma reação “” na vertical;
- E que o apoio fixo em vai realizar uma reação “” na horizontal (que vai acabar sendo nula e pode ser omitida do diagrama de corpo livre) e uma reação “” na vertical,
...o nosso DCL (diagrama de corpo livre) fica assim:
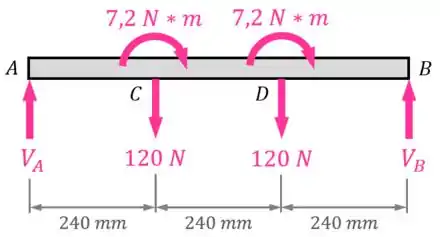
Passo 2
Feito o DCL, o próximo ingrediente ou passo da nossa resolução é o:

Aqui, temos duas condições de equilíbrio que podemos aplicar:
- O equilíbrio de forças na vertical;
- E o equilíbrio de momentos em relação a um ponto.
Aplicando o equilíbrio de forças na vertical, temos:
E realizando esse somatório, encontramos que:
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto :
Em relação à esse ponto, vamos ter os seguintes momentos atuando:
- O momento no sentido anti-horário () gerado por com um braço de ;
- Os momentos no sentido horário () gerados pelas forças de em e em , com braços de e , respectivamente;
- E os momentos concentrados em e em de .
Dessa forma, o somatório de momentos fica assim:
Isolando , encontramos que:
E, substituindo esse valor na expressão que encontramos anteriormente, encontramos que:
Passo 3
Agora que já conhecemos todos os esforços (forças e momentos) externos atuantes na nossa viga, podemos seguir para o próximo ingrediente de uma boa resolução, que é a:

Existem descontinuidades (nesse caso, forças e momentos concentrados) nos pontos , , e dessa viga.
Então temos que analisar os esforços internos nas seções entre e , nas seções entre e e nas seções entre e da viga:
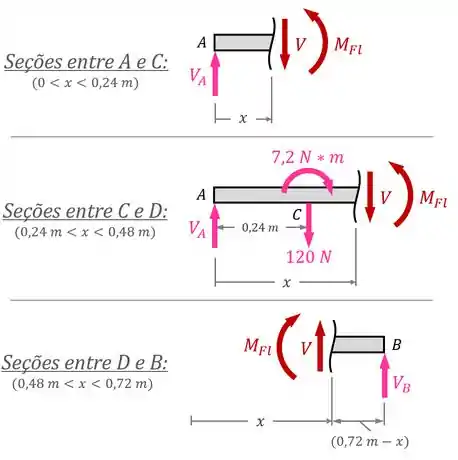
Feitos esses desenhos, precisamos aplicar as condições de equilíbrio em cada situação para terminar a análise.
Para as seções entre e , temos o equilíbrio de forças na vertical:
Que nos diz que:
E também temos o equilíbrio de momentos em relação ao ponto da seção:
Que nos diz que:
Isolando e substituindo , encontramos que:
Em seguida, para as seções entre e , o equilíbrio de forças na vertical fica assim:
Isolando e substituindo , encontramos que:
E o equilíbrio de momentos em relação ao ponto da seção fica assim:
Isolando , temos:
Substituindo e fazendo a distributiva em “”, temos:
O que significa que:
Por fim, para as seções entre e , o equilíbrio de forças fica assim:
O que nos diz que:
Enquanto que o equilíbrio de momentos fica assim:
Isolando e substituindo , temos que:
Fazendo a distributiva, isso nos diz que:
E assim terminamos a análise dos esforços internos!

Passo 4
Mas espera, ainda faltam os:

Bora lá fazer eles!
Encontramos no passo anterior que, nos diferentes trechos da nossa viga, a força cortante assume os valores , e .
Então o diagrama da força cortante fica assim:
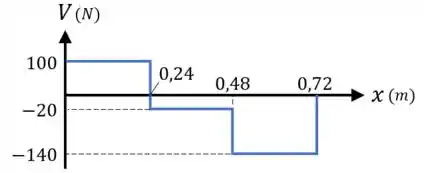
E desse diagrama, ainda observamos que o valor máximo absoluto da força cortante é:
Em seguida, para o momento fletor , temos 3 equações.
De acordo com a primeira:
...o momento fletor varia linearmente entre e .
De acordo com a segunda:
...o momento fletor varia linearmente entre e .
E, por fim, de acordo com a terceira:
...o momento fletor varia linearmente entre e .
Dessa forma, o diagrama do momento fletor fica assim:
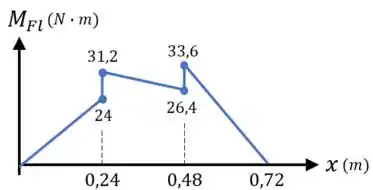
E desse diagrama, ainda observamos que o valor máximo absoluto do momento fletor é:
E pronto!
Finalizamos assim o exercício e o resultado de todo esse trabalho é um:
