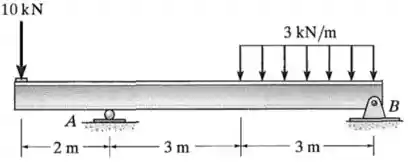
A viga está sujeita ao carregamento mostrado. Represente graficamente os diagramas de força cortante e momento fletor.
Passo 1
O exercício quer que a gente esboce os diagramas da força cortante e do momento fletor na viga da figura.
Como sempre, o primeiro elemento de uma resolução de um exercício desse tipo é o:

Nesse caso:
- O apoio móvel em vai realizar somente uma reação na vertical;
- E o apoio fixo em vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do diagrama de corpo livre) e uma reação na vertical.
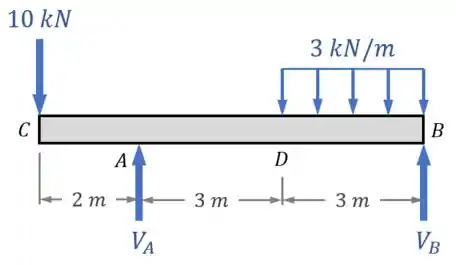
Dessa forma, o nosso DCL (diagrama de corpo livre) fica assim:
Passo 2
Feito o DCL, podemos seguir para o próximo elemento da resolução, que é o:

Aqui, podemos aplicar:
- O equilíbrio de forças na vertical;
- E o equilíbrio de momentos em relação a um ponto.
Aplicando o equilíbrio de forças na horizontal, temos:
Para fazer esse somatório de forças, precisamos da força equivalente à carga distribuída de .
Como ela está distribuída ao longo de um comprimento de , temos que a sua força equivalente vai ser:
Dessa forma, o somatório de forças fica assim:
O que significa que:
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto (lembre-se de que você pode aplicar em relação a qualquer ponto, ok? Para este caso, eu achei que o ponto ficaria mais simples):
Em relação ao ponto , vamos ter:
- Um momento no sentido anti-horário () gerado pela distribuição uniforme de , que age com uma força equivalente de no meio da região da distribuição, tendo um braço de em relação ao ponto , como mostra a imagem abaixo:
- Um momento no sentido horário () gerado por com um braço de ;
- E um momento no sentido anti-horário () gerado pela força de com um braço de .
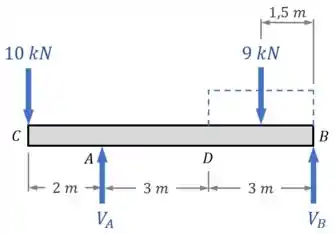
Dessa forma, o somatório de momentos fica assim:
Isolando , encontramos que:
E, substituindo isso na expressão que encontramos anteriormente, encontramos que:
Passo 3
Agora que conhecemos todos os esforços (forças e momentos) externos atuantes na nossa viga, podemos seguir para o próximo elemento da resolução, a:

Na nossa viga, existem descontinuidades (nesse caso, forças concentrados ou o início ou fim de forças distribuídas) nos pontos , e e .
Então devemos analisar as seções entre e , as seções entre e e as seções entre e :
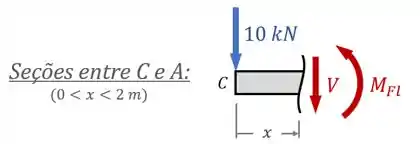
Para as seções entre e , o equilíbrio de forças na vertical:
...nos diz que:
Enquanto que o equilíbrio de momentos:
...nos diz que:
Show!
1ª situação analisada!
![]()
Passo 4
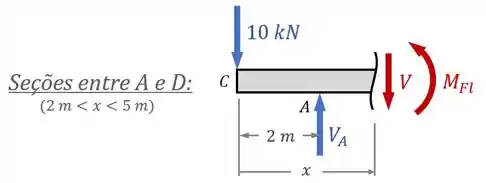
Já para as seções entre e , o equilíbrio de forças na vertical fica assim:
Isolando e substituindo , temos que:
Enquanto que o equilíbrio de momentos fica assim:
Isolando , temos:
Substituindo e fazendo a distributiva, obtemos que:
O que significa que:
Pronto!
2ª situação analisada!

Passo 5
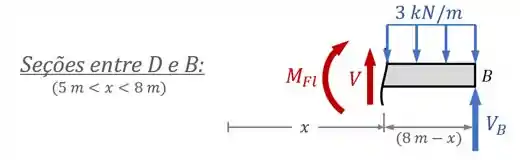
obs: Pessoal, repararam que na última seção a gente fez o corte da direita para a esquerda? Isso foi feito para simplificar o cálculo e não precisar ficar escrevendo todas as forças novamente. A única coisa que temos de lembrar é que os sentidos de e vão se inverter, fora isso é tudo igualzinho!
Por fim, para as seções entre e , o equilíbrio de forças fica assim:
Isolando , temos:
Fazendo a distributiva e substituindo , encontramos que:
Quanto ao equilíbrio de momentos em relação ao ponto da seção:
...precisamos perceber que a força distribuída de vai gerar um momento no sentido horário () com uma força equivalente de e um braço de .
Dessa forma, o somatório de momentos fica assim:
Isolando , temos:
Desenvolvendo essa expressão e substituindo , temos:
Arrumando isso, encontramos que:
Rá!
![]()
3ª Situação Analisada! Terminamos a análise dos esforços internos.
Passo 6
Por fim, chegamos ao último elemento da resolução, que são os:

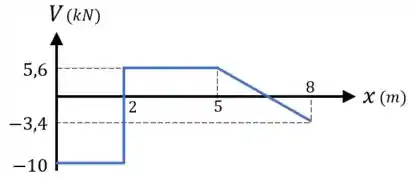
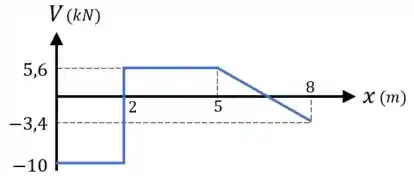
Para a força cortante , temos:
- Que ela é de quando ;
- Que ela é de quando ;
- E que ela segue a equação quando , variando linearmente entre e .
Dessa forma, o diagrama da força cortante fica assim:
Passo 7
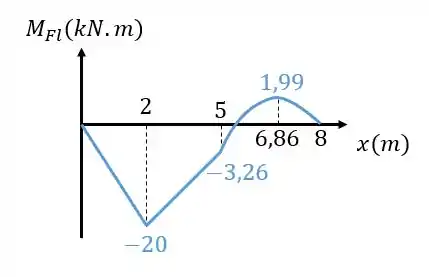
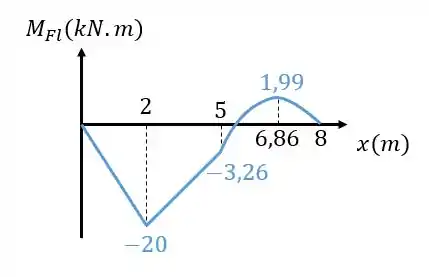
Para o momento fletor , temos que:
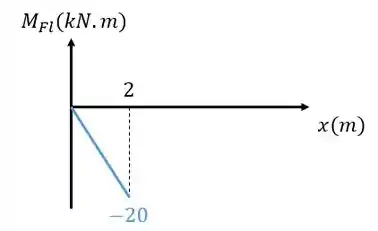
- Ele varia linearmente de acordo com a equação:
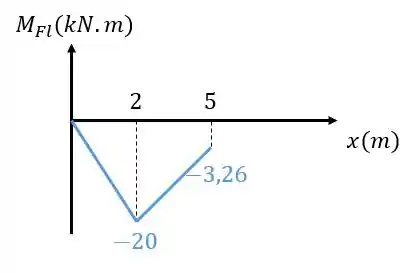
- Ele varia linearmente de acordo com
- E que ele varia de acordo com a função quadrática
entre os pontos e ;
entre os pontos e ;
entre os pontos e .
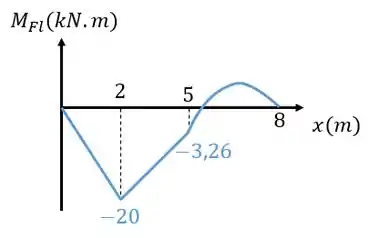
Para completar o diagrama de momento fletor, é interessante saber qual é o valor máximo ou mínimo de quando ele varia de acordo com a função quadrática no trecho .
Para tanto, podemos derivar e igualar à zero a função quadrática :
Isolando nessa expressão acima, conseguimos descobrir o ponto de máximo ou mínimo da função quadrática:
Substituindo esse valor na função quadrática, conseguimos calcular o seu valor de máximo ou mínimo:
Sabendo disso, podemos finalmente esboçar o nosso diagrama completo do momento fletor:
Resposta