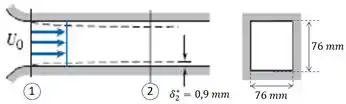
Ar escoa na região de entrada de um duto quadrado, conforme mostrado. A velocidade é uniforme, , e o duto tem área de . Em uma seção a a jusante da entrada, a espessura de deslocamento, , em cada parede mede . Determine a variação de pressão entre as seções e.
Passo 1
E aí, entendeu o problema? O enunciado nos pede para calcular a diferença de pressão entre os dois pontos. Mas por que há essa diferença? Chegou a pensar nisso?
Sabemos que pressão e velocidade estão correlacionados pela equação de Bernoulli:
Então, para que exista uma diferença de pressão entre e , significa dizer que há também uma diferença entre as velocidades médias dos pontos e . E você saberia explicar o porquê dessa diferença de velocidades?
Para isso, temos que lembrar da definição de espessura de deslocamento (). Ela é a distância da qual a superfície deve ser deslocada, tal que o fluxo volumétrico real possa ser calculado por meio de um perfil uniforme (velocidades constantes).
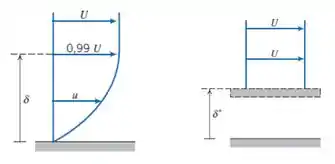
Como nos foi dado o valor dessa espessura, podemos considerar o escoamento nesse duto como se ele fosse em um duto convergente, ou seja, cuja área diminui ao longo do escoamento:
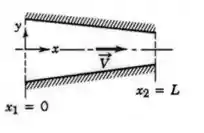
Como a vazão é constante, sabemos que ao diminuir a área do escoamento, aumentamos a velocidade média do fluido e, consequentemente, diminuímos a pressão. Sendo assim, esperamos que .
Vamos conferir se isso condiz com o resultado?
Passo 2
Pela equação da conservação da massa, admitindo estado estacionário, temos que:
Sendo assim:
Como as velocidades e são constantes:
O cálculo das áreas será dado por:
Já sabemos que no início (ponto ), a camada-limite ainda não se formou e a velocidade média do escoamento equivale à do fluido antes de entrar (. Dessa maneira:
Passo 3
Pela equação de Bernoulli aplicada aos pontos e :
Olha que bacana! De fato, a diferença de pressão deu negativa como havíamos predito ao início!
Então aprendemos que: em dutos com contração, a velocidade média aumenta ao longo do escoamento e que, em regiões com maiores velocidades, observamos menores valores de pressão (para um determinado sistema com energia fixada).