Exercícios Resolvidos de Espessura de Camada-Limite

Enunciado

Os perfis de velocidade das camadas-limite laminares frequentemente são aproximados pelas equações

Linear:

Senoidal:

Parabólico:

Compare as formas destes perfis de velocidade, traçando um gráfico de (na ordenada) como uma função de (na abscissa).

Passo 1

Nesse exercício já temos o comportamento de três tipos de camadas-limite laminares. Isso já é um adianto o/

Para traçar o gráfico, vamos pegar alguns valores de y e aplicar as fórmulas dadas no enunciado separadamente. Os valores estão na tabela

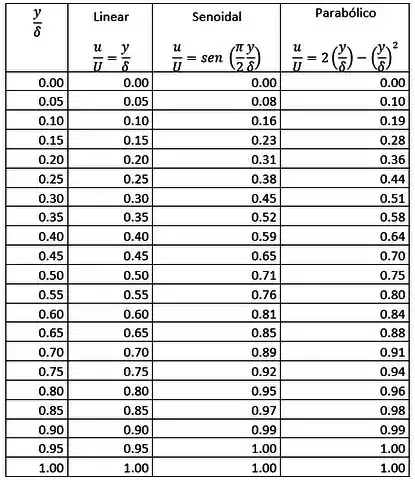
Por último, vamos fazer o gráfico com esses valores. Antes, atençãããão! O eixo y será a distância adimensional, ou seja, . E no eixo x estarão as velocidades adimensionais (u/U).

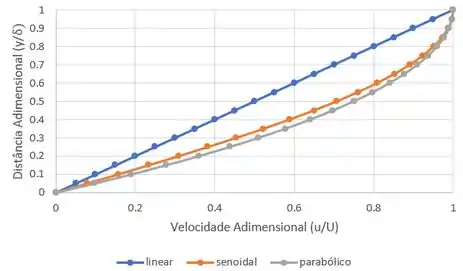
E assim conseguimos aproximar camadas-limites laminares como essa:

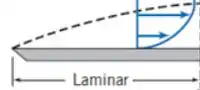
Nesse caso, o comportamento que melhor se encaixa é o parabólico ou o senoidal 😉

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Como um caso semelhante ao do Exemplo 7.5, Howarth também propôs a distribuição de velocidades com gradiente adverso U = U 0 ( 1 - x 2 L 2 ) e calculou a separação em x s e pL = 0,271 por um método de

Em 1957, H. Görtler propôs os seguintes casos-teste com gradientes adversos U = U 0 1 + x L η e calculou a separação para escoamento laminar caso η = 1 como x s e p L = 0,159 . Compare com o método de

Para escoamento de ar padrão ao nível do mar a 4m / s paralelo a uma placa plana fina, calcule a espessura da camada-limite em x = 60c m a partir do bordo de ataque:

Uma chapa fina de fibra pesa 90 N e se localiza sobre o topo de um telhado, como mostra a Figura P7.45. Considere ar ambiente a 20°C e 1 atm. Se o coeficiente de atrito sólido entre a chapa e o telhad

No Problema F E 7.4 , para as mesmas condições de escoamento, qual é a tensão de cisalhamento na parede em x = 60c m a partir do bordo de ataque?