Um fluido de massa, específica , escoa a sobre uma placa plana de de comprimento e de largura. Na borda de fuga, a espessura da camada-limite é . Considere que o perfil de velocidade é linear, conforme mostrado, e que o escoamento é bidimensional (as condições de escoamento são independentes de ). Usando o volume de controle , mostrado por linhas tracejadas:
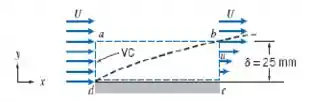
Calcule a vazão através da superfície .
Determine a força de arrasto sobre a superfície superior da placa.
Passo 1
Vamos inicialmente organizar nossos objetivos! O enunciado nos pede 2 coisas: a vazão de fluido através da superfície e a força de arrasto sobre a superfície.
O cálculo da vazão é feito pelo balanço de massa que já vimos anteriormente no tópico de Forma Integral do Volume de Controle:
Note que precisaremos do perfil de velocidades para calcular a vazão, mas qual é sua expressão?
O enunciado nos diz que o perfil é linear, logo é do tipo:
Lembra das condições de contorno? Então, sabemos que a velocidade é nula em e que equivale a em . Portanto:
E ainda:
Pronto! Temos que o perfil de velocidades é dado por:
Podemos reescrevê-lo com a variável :
Passo 2
Considerando o retângulo como volume de controle (VC) e que o problema está no estado estacionário (propriedades não variam no tempo), podemos escrever:
Como são e são constantes, podem sair das derivadas e integrais:
Substituindo a expressão do perfil de velocidades que encontramos:
Pela mudança de variável, temos:
Logo:
Substituindo na integral:
Passo 3
Vamos agora concluir nosso segundo objetivo: determinar a força de arrasto que a superfície da placa sofre devido ao escoamento do fluido.
Se antes utilizamos o balanço de massa para encontrar a vazão, agora, como queremos encontrar uma força, utilizaremos o balanço de momento:
Como assumimos estado estacionário e o volume de controle não se move simultaneamente ao fluido ():