Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Espessura de Camada-Limite

Ver Teoria
Exercício 31245678

Enunciado

Avalie δ * / δ e θ / δ para o perfil de velocidade turbulento da lei de potência 1/7 apresentado abaixo. Compare com as razões para o perfil parabólico de velocidade de camada-limite laminar dado.

Lei de Potência 1/7: u U ∞ = y δ 1 / 7

Parabólico: u U ∞ = 2 y δ - y δ 2

Passo 1

Nesse exercício queremos comparar as espessuras das camadas limites para duas diferentes formas: uma laminar e outra turbulenta.

Para o perfil turbulento, foi dada uma lei de potência que fornece uma camada mais achatada, enquanto no perfil laminar, ela é mais acentuada

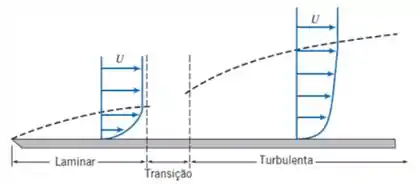
Pela figura já podemos esperar que a relação entre as espessuras da laminar será maior que a da turbulenta.

Vamos verificar isso em números tanto para a espessura de deslocamento δ * em relação a de perturbação δ como para a espessura de quantidade de movimento θ em relação a δ

Para a espessura de deslocamento, temos essa equação

δ * = ∫ 0 δ 1 - u U ∞ d y

Dividindo pela espessura de perturbação δ já que queremos encontrar essa razão

δ * δ = 1 δ ∫ 0 δ 1 - u U ∞ d y

Fazendo uma mudança de variáveis para facilitar a solução da integral

η = y δ ⇒ d η = 1 δ d y

d y =   δ d η

P a r a   y   =   δ   →   η   =   1

Atualizando a equação

δ * δ = 1 δ ∫ 0 1 1 - u U ∞ δ d η

δ * δ = ∫ 0 1 1 - u U ∞ d η

Agora vamos analisar o perfil de lei de potência 1/7 turbulento e substituir a nova variável

u U ∞ = y δ 1 / 7 = η 1 / 7

Voltando à equação

δ * δ = ∫ 0 1 1 - η 1 / 7 d η

Resolvendo

δ * δ = ∫ 0 1 d η - ∫ 0 1 η 1 / 7 d η

δ * δ = η - η 8 / 7 8 / 7 0 1

δ * δ = 1 - 7 8 = 1 8 = 0,125

Encontramos a razão entre a espessura de deslocamento e a de perturbação para o perfil turbulento. Vamos comparar com o laminar parabólico

u U ∞ = 2 y δ - y δ 2 = 2 η - η 2

Substituindo na equação da espessura de deslocamento

δ * δ = ∫ 0 1 1 - u U ∞ d η

δ * δ = ∫ 0 1 1 - 2 η + η 2 d η

Integrando

δ * δ = η - η 2 + η 3 3 0 1

δ * δ = 1 - 1 + 1 3

Então, a relação entre as espessuras no perfil parabólico é

δ * δ = 1 3 ≈ 0,3333

Com isso, vemos que a relação δ * / δ   é

δ * δ = 0,125   ( t u r b u l e n t o   l e i   d e   p o t ê n c i a )

δ * δ ≈ 0,333   ( l a m i n a r   p a r a b ó l i c o )

Ou seja, a espessura da camada-limite de deslocamento em relação a de perturbação é menor para o escoamento turbulento, como esperávamos :D

Passo 2

Agora vamos analisar a espessura de quantidade de movimento, definida assim:

θ = ∫ 0 δ u U ∞ · 1 - u U ∞ d y

Dividindo pela espessura de perturbação

θ δ = 1 δ ∫ 0 δ u U ∞ · 1 - u U ∞ d y

Utilizando a variável η = y δ

θ δ = ∫ 0 1 u U ∞ · 1 - u U ∞ d η

Finalmente, vamos substituir os perfis de velocidade. Primeiro, o turbulento

u U ∞ = y δ 1 / 7 = η 1 / 7

θ δ = ∫ 0 1 η 1 / 7 · 1 - η 1 / 7 d η

θ δ = ∫ 0 1 η 1 / 7 d η - ∫ 0 1 η 2 / 7 d η

θ δ = η 8 / 7 8 / 7 - η 9 / 7 9 / 7 0 1

θ δ = 7 8 - 7 9 = 7 72

A relação entre espessura de quantidade de movimento e de perturbação no perfil turbulento estudado é

θ δ ≈ 0,0972

Analisando o perfil parabólico laminar

u U ∞ = 2 y δ - y δ 2 = 2 η - η 2

Substituindo em θ δ = ∫ 0 1 u U ∞ · 1 - u U ∞ d η

θ δ = ∫ 0 1 2 η - η 2 · 1 - 2 η - η 2 d η

θ δ = ∫ 0 1 2 η - 5 η 2 + 4 η 3 - η 4 d η

Integrando

θ δ = η 2 - 5 3 η 3 + 4 4 η 4 - 1 5 η 5 0 1

θ δ = 1 - 5 3 + 1 - 1 5

Então, a relação entre as espessuras no perfil parabólico é

θ δ = 2 15 ≈ 0,1333

Com isso, encontramos todas as relações como esperado, a relação no escoamento laminar é maior que no escoamento turbulento.

Resposta

Parabólico Laminar:

δ * δ = 1 3 ≈ 0,3333

θ δ = 2 15 ≈ 0,1333

Lei de potências 1/7 Turbulento:

δ * δ = 0,125

θ δ ≈ 0,0972

Exercícios de Livros Relacionados

Como um caso semelhante ao do Exemplo 7.5, Howarth também propôs a distribuição de velocidades com gradiente adverso U = U 0 ( 1 - x 2 L 2 ) e calculou a separação em x s e pL = 0,271 por um método de
Em 1957, H. Görtler propôs os seguintes casos-teste com gradientes adversos U = U 0 1 + x L η e calculou a separação para escoamento laminar caso η = 1 como x s e p L = 0,159 . Compare com o método de
Para escoamento de ar padrão ao nível do mar a 4m / s paralelo a uma placa plana fina, calcule a espessura da camada-limite em x = 60c m a partir do bordo de ataque:
Uma chapa fina de fibra pesa 90 N e se localiza sobre o topo de um telhado, como mostra a Figura P7.45. Considere ar ambiente a 20°C e 1 atm. Se o coeficiente de atrito sólido entre a chapa e o telhad
No Problema F E 7.4 , para as mesmas condições de escoamento, qual é a tensão de cisalhamento na parede em x = 60c m a partir do bordo de ataque?