Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fator de Forma

Ver Teoria
Exercício 12345678

Enunciado

(Adaptado) Determine F 1 → 2 , F 2 → 1 , F 3 → 2 , F 2 → 2 e F 2 → 3 para a configuração hemisfera-disco abaixo usando a regra da reciprocidade e outras relações básicas do fator de forma.

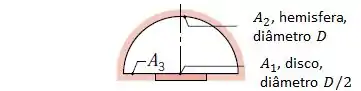
Não utilize tabelas ou gráficos.

Passo 1

Como o disco A 1 e a coroa circular A 3 estão no mesmo plano, a radiação emitida por uma não irá incidir sobre a outra, ou sobre ela mesma, logo:

F 1 → 1 = 0

F 1 → 3 = 0

F 3 → 3 = 0

F 3 → 1 = 0

Sendo assim, aplicando a regra da adição a essas duas superfícies:

F 1 → 1 + F 1 → 2 + F 1 → 3 = 1

F 1 → 2 = 1

F 3 → 1 + F 3 → 2 + F 3 → 3 = 1

F 3 → 2 = 1

Passo 2

Aplicando a regra da reciprocidade para encontrar F 2 → 3 :

F 2 → 3 = F 3 → 2 . A 3 A 2

F 2 → 3 = F 3 → 2 × π 4 D 2 - D 2 2 π D 2 2

F 2 → 3 = 1 × π 4 D 2 - D 2 4 × 2 π D 2

F 2 → 3 = 1 2 D 2 3 D 2 4

F 2 → 3 = 3 8

F 2 → 3 = 0,375

Passo 3

Aplicando a regra da reciprocidade para encontrar F 2 → 1 :

F 2 → 1 = F 1 → 2 . A 1 A 2

F 2 → 1 = F 1 → 2 × π 4 D 2 2 π D 2 2

F 2 → 1 = 1 × π D 2 16 × 2 π D 2

F 2 → 1 = 1 8

F 2 → 1 = 0,125

Passo 4

Utilizando a regra da adição para a superfície A 2 :

F 2 → 1 + F 2 → 2 + F 2 → 3 = 1

F 2 → 2 = 1 - F 2 → 1 - F 2 → 3

Substituindo os valores:

F 2 → 2 = 1 - 0,125 - 0,375

F 2 → 2 = 0,5

Resposta

F 1 → 2 = 1

F 3 → 2 = 1

F 2 → 3 = 0,375

F 2 → 1 = 0,125

F 2 → 2 = 0,5

Exercícios de Livros Relacionados

A configuração mostrada é usada para calibrar um medidor de fluxo térmico. O medidor tem uma superfície negra com 10 mm de diâmetro, que é mantida a 17°C por uma placa de suporte resfriada com água. O
Uma amostra aquecida eletricamente é mantida com uma temperatura superficial Ta = 500 K. O revestimento da amostra é difuso, porém espectralmente seletivo, com a distribuição da emissividade espectral
Uma pista de patinação no gelo circular com 25m de diâmetro encontra-se coberta por uma cúpula hemisférica com 35m de diâmetro. Se as superfícies do gelo e da cúpula puderem ser aproximadas por corpos
Como mostrado na figura, considere o disco A 1 localizado coaxialmente a 1m de distância, porém inclinado 30 ° em relação à reta normal a uma coroa circular A 2 . Qual é a irradiação sobre A 1 devido
Considere duas superfícies difusas A 1 e A 2 no interior de uma cavidade esférica com raio R . Usando os métodos a seguir, deduza uma expressão para o fator de forma F 12 em termos de A 2 e R .(a) Det