Uma peça longa em forma de é tratada termicamente pela sua suspensão no interior de um forno tubular com diâmetro de e uma temperatura de parede de . O tem os lados com de comprimento e um ângulo de .
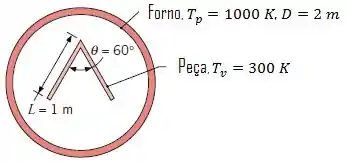
Se a parede do forno e as superfícies da peça puderem ser aproximadas por corpos negros e a peça se encontra a uma temperatura inicial de , qual é a taxa líquida de transferência de calor por radiação por unidade de comprimento da peça?
Passo 1
Se trabalharmos com cada aba da peça e a esfera, teremos um sistema de três corpos, vamos conseguir resolver o problema, mas teremos um certo trabalho, já que a transferência de calor se dá dos dois lados de cada aba.
Uma estratégia que pode ajudar bastante nesse caso é, ao invés de separarmos a peça em pelas abas, vamos separá-la a partir de suas superfícies interna e externa, tratando cada uma como um corpo, que está à mesma temperatura.
Assim, sendo 1 a superfície interna do , 2 a superfície externa do e a superfície cilíndrica do redor, podemos escrever a taxa de transferência de calor por radiação como:
Vamos tratar dos fatores de forma, agora.
Passo 2
Olhando para a superfície externa do , qualquer radiação emitida por ela não incide sobre ela mesmo e nem sobre a superfície interna do , sendo assim:
Dessa forma, pela regra da adição, teremos:
Usando a regra da reciprocidade, teremos:
![]()
Passo 3
Analisando a superfície interna do , nenhuma radiação emitida por ele irá incidir sobre a superfície externa, logo:
O fator de forma pode ser calculado a partir da seguinte equação tabelada:
Utilizando a regra da adição, teremos:
Utilizando a regra da reciprocidade:
![]()
Passo 4
Voltando à equação da taxa de transferência de calor:
Substituindo os valores, teremos: