Considere discos negros, paralelos coaxiais, separados por uma distância de . O disco inferior, com diâmetro de , é mantido a , enquanto a vizinhança está a .
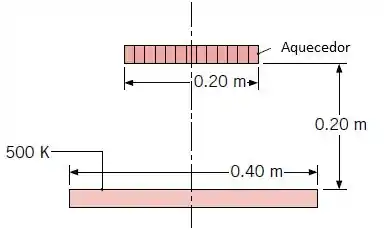
Qual será a temperatura que o disco superior, com diâmetro de , irá atingir se uma potência elétrica de for suprida ao aquecedor que se encontra na sua parte posterior?
Passo 1
A potência elétrica deve ser igual à soma das transferências de calor para o disco superior. Assim:
Onde o índice 2 está relacionado ao disco inferior e o índice 3 está relacionado à vizinhança.
Dessa equação, nós temos praticamente tudo o que precisamos, exceto os fatores de forma, então vamos atrás deles.
Passo 2
Começando pelo fator de forma , temos um gráfico que pode resolver a nossa vida mas, pra isso, precisamos calcular as seguintes grandezas:
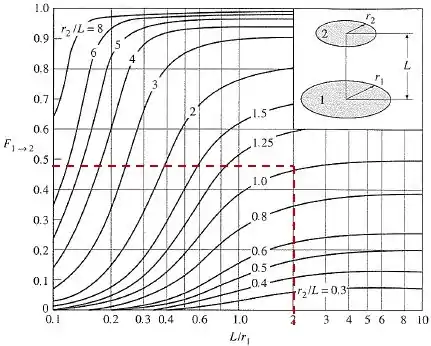
![]()
Passo 3
Pela regra da adição:
Como o disco é uma superfície plana, nenhuma radiação emitida por ele irá incidir sobre ele mesmo. Assim:
Logo:
![]()
Passo 4
Voltando à equação que encontramos no Passo 1:
Substituindo os valores:
Jogando isso tudo na calculadora, teremos:
![]()