(Adaptado) Determine e para a pequena esfera com área sob uma hemisfera concêntrica com área , usando a regra da reciprocidade e outras relações básicas do fator de forma.
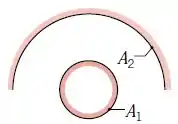
Não utilize tabelas ou gráficos.
Passo 1
Nesse tipo de casos, a melhor estratégia é “fechar” o desenho, isso costuma ajudar muito a resolver o problema.
Sendo assim, vamos inventar uma hemisfera com área para fechar a hemisfera do desenho, se liga:
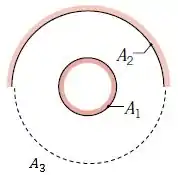
Pela regra da adição, temos que:
No entanto, como se trata de uma esfera, a superfície não consegue emitir nenhuma radiação que incida sobre ela mesma, logo:
Além disso, como a hemisfera que inventamos (em pontilhado) é igual à hemisfera , podemos afirmar que:
Sendo assim:
Passo 2
Utilizando a regra da reciprocidade:
Segundo o enunciado , logo:
Resposta
Exercícios de Livros Relacionados
A configuração mostrada é usada para calibrar um medidor de fluxo térmico. O medidor tem uma superfície negra com 10 mm de diâmetro, que é mantida a 17°C por uma placa de suporte resfriada com água. O
Uma amostra aquecida eletricamente é mantida com uma temperatura superficial Ta = 500 K. O revestimento da amostra é difuso, porém espectralmente seletivo, com a distribuição da emissividade espectral
Uma pista de patinação no gelo circular com 25m de diâmetro encontra-se coberta por uma cúpula hemisférica com 35m de diâmetro. Se as superfícies do gelo e da cúpula puderem ser aproximadas por corpos
Como mostrado na figura, considere o disco A 1 localizado coaxialmente a 1m de distância, porém inclinado 30 ° em relação à reta normal a uma coroa circular A 2 . Qual é a irradiação sobre A 1 devido
Considere duas superfícies difusas A 1 e A 2 no interior de uma cavidade esférica com raio R . Usando os métodos a seguir, deduza uma expressão para o fator de forma F 12 em termos de A 2 e R .(a) Det