Uma cavidade cilíndrica com diâmetro e profundidade é usinada em um bloco de metal, e as condições são tais que as suas superfícies da base e lateral são mantidas a e , respectivamente.
Aproximando as superfícies por superfícies negras, determine o poder emissivo da cavidade se e .
Passo 1
A ideia é basicamente essa:
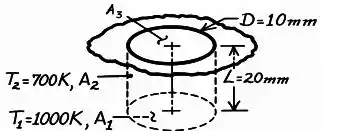
Por definição, o poder emissivo da cavidade é dado por:
Onde é dado por:
Para resolver o problema, vamos precisar dos fatores de forma.
Passo 2
Pela regra da simetria, podemos dizer que:
![]()
E através da regra da reciprocidade, podemos dizer que
![]()
Por último, pela regra da adição:
Onde , já que, como a base é plana, nenhuma radiação emitida por ela irá incidir sobre ela mesma, logo:
![]()
Juntando todas as informações, teremos que:
![]()
Assim, a equação da taxa de transferência de radiação será:
E o poder emissivo será dado por:
Como :
Passo 3
Para calcular o fator de forma , vamos usar o gráfico, onde:
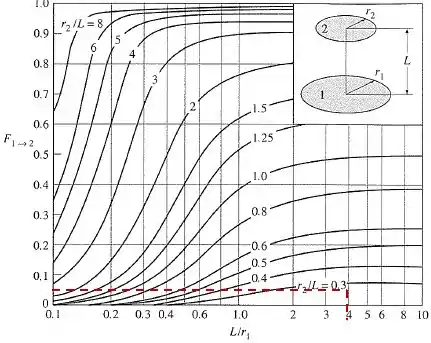
![]()
Passo 4
Substituindo os valores:
![]()